Volume d’un ellipsoïde: Calculateur en ligne, définition, formule, méthode de calcul, domaines d’application et exercices corrigés
Calculateur du volume d’un ellipsoïde
Pour faciliter le calcul du volume d’un ellipsoïde, vous pouvez utiliser un calculateur ci-dessous. Il permettent de saisir les demi-axes de l’ellipsoïde et d’obtenir instantanément le volume correspondant.
Introduction :
L’ellipsoïde est une forme géométrique tridimensionnelle qui ressemble à une sphère étirée dans différentes directions. Connaître le volume d’un ellipsoïde peut être utile dans de nombreux domaines, tels que la géométrie, la physique ou l’ingénierie. Cet article vous guidera à travers la formule de calcul du volume d’un ellipsoïde et expliquera comment l’utiliser de manière pratique.
Formule du volume d’un ellipsoïde
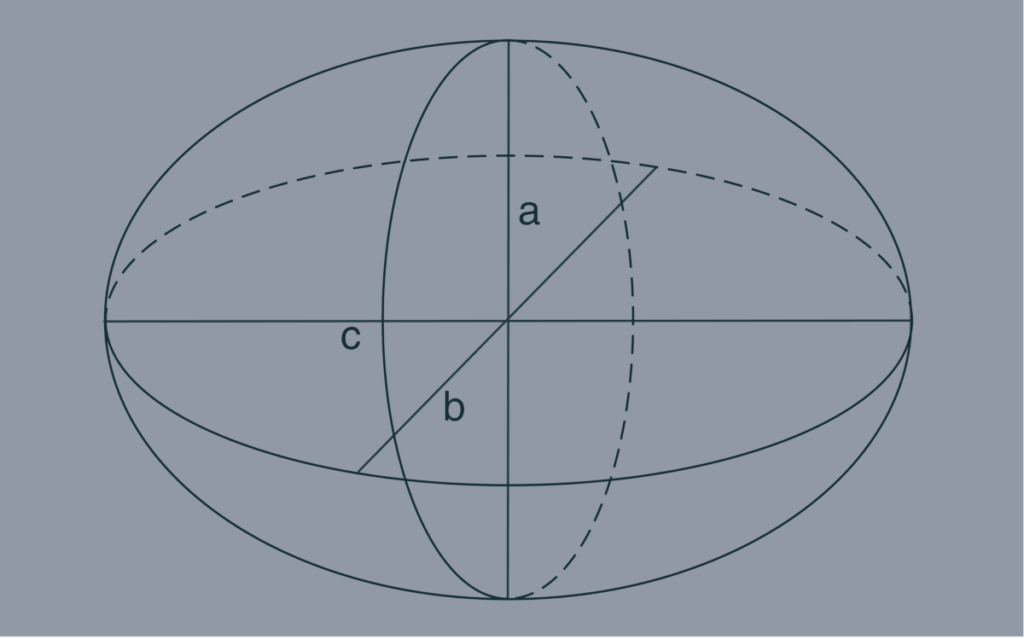
Le volume V d’un ellipsoïde peut être calculé en utilisant la formule suivante :
V = (4/3) × π × a × b × c
Dans cette formule, a, b et c représentent les demi-axes de l’ellipsoïde. Les demi-axes correspondent aux distances du centre de l’ellipsoïde aux points situés sur les axes principal, moyen et mineur. Ils peuvent également être considérés comme les rayons de la sphère dont l’ellipsoïde est une approximation.
Méthode de calcul
Pour calculer le volume d’un ellipsoïde, suivez ces étapes simples :
- Mesurez les demi-axes : Prenez un ellipsoïde et mesurez les longueurs des demi-axes a, b et c. Assurez-vous que les mesures sont cohérentes et exprimées dans la même unité (par exemple, centimètres).
- Appliquez la formule : Prenez les valeurs mesurées des demi-axes et substituez-les dans la formule du volume d’un ellipsoïde :
V = (4/3) × π × a × b × c
- Calculez le volume : Effectuez les opérations mathématiques nécessaires pour trouver la valeur du volume. N’oubliez pas d’utiliser une valeur précise de π, telle que 3.14159, pour obtenir des résultats plus précis.
Applications des ellipsoïdes
Les ellipsoïdes ont de nombreuses applications dans divers domaines scientifiques et technologiques. Voici quelques exemples d’applications courantes des ellipsoïdes :
- Géodésie et géophysique : Les ellipsoïdes sont utilisés pour modéliser la forme de la Terre. Le modèle géodésique de référence le plus largement utilisé, appelé ellipsoïde de référence ou ellipsoïde de révolution, est utilisé pour représenter la Terre de manière simplifiée. Cela permet de calculer les coordonnées géographiques, d’établir des systèmes de référence géodésiques et de mesurer des distances sur la surface de la Terre.
- Optique : Les ellipsoïdes sont utilisés en optique pour modéliser les formes des miroirs, des lentilles et des réflecteurs. L’utilisation d’ellipsoïdes permet de contrôler et de focaliser la lumière de manière efficace, ce qui est essentiel dans la conception d’appareils optiques tels que les télescopes, les microscopes et les dispositifs de focalisation optique.
- Mécanique des fluides : Les ellipsoïdes sont utilisés pour décrire le mouvement des particules dans les fluides. En utilisant des ellipsoïdes allongés ou aplaties, on peut modéliser la trajectoire des particules dans des écoulements turbulents ou dans des conditions spécifiques. Cela permet de comprendre et d’étudier le comportement des fluides dans diverses applications, telles que l’aérodynamique, l’hydrodynamique et la dynamique des particules.
- Géophysique et sismologie : Les ellipsoïdes sont utilisés pour modéliser les déformations de la croûte terrestre causées par des contraintes tectoniques et sismiques. Les ellipsoïdes de déformation sont utilisés pour décrire et prédire les mouvements et les déformations de la Terre lors de tremblements de terre et d’autres événements géophysiques. Ils permettent de mieux comprendre les processus tectoniques et les contraintes exercées sur la croûte terrestre.
- Conception de navires et d’aéronefs : Les ellipsoïdes sont utilisés dans la conception et l’analyse de navires et d’aéronefs pour modéliser la résistance hydrodynamique et aérodynamique. Les ellipsoïdes permettent de calculer la traînée et les forces appliquées aux structures, ce qui est essentiel pour optimiser la conception et les performances des navires et des aéronefs.
- Mathématiques et physique : Les ellipsoïdes sont étudiés en tant qu’objets mathématiques dans la géométrie différentielle et la théorie des surfaces. Ils sont également utilisés dans des domaines de la physique tels que la mécanique quantique et la thermodynamique pour modéliser des systèmes physiques complexes et décrire des propriétés quantitatives.
Ces applications illustrent l’importance des ellipsoïdes dans divers domaines scientifiques et technologiques. Leur forme géométrique unique et leurs propriétés mathématiques en font des outils précieux pour la modélisation, l’analyse et la compréhension de phénomènes complexes.
Exercices corrigés
Exercice 1 :
Un ellipsoïde a des demi-axes mesurant a = 8 cm, b = 6 cm et c = 4 cm. Calculez son volume.
Solution :
V = (4/3) × π × a × b × c
V = (4/3) ×3.14159×8×6×4
V ≈ 804.2477 cm³
Donc, le volume de l’ellipsoïde est d’environ 804.2477 cm³.
Exercice 2 :
Un ellipsoïde a des demi-axes mesurant a = 12 cm, b = 10 cm et c = 7 cm. Trouvez son volume.
Solution :
V = (4/3) × π × a × b × c
V = (4/3) ×3.14159 ×12×10×7
V ≈ 3951.859 cm³
Le volume de l’ellipsoïde est d’environ 3951.859 cm³.
Exercice 3 :
Un ellipsoïde a un volume de 2000 cm³. Les demi-axes b et c mesurent 5 cm et 8 cm respectivement. Trouvez la valeur du demi-axe a.
Solution :
On peut réorganiser la formule du volume pour trouver a :
V = (4/3) × π × a × b × c
a = V / ((4/3) ×π ×b×c)
a = 2000 / ((4/3) × 3.14159×5×8)
a ≈ 15.923 cm
Le demi-axe a de l’ellipsoïde mesure environ 15.923 cm.
Conclusion
Le calcul du volume d’un ellipsoïde est relativement simple en utilisant la formule appropriée. En mesurant les demi-axes et en les substituant dans la formule, vous pouvez obtenir rapidement et facilement le volume de l’ellipsoïde. N’oubliez pas de choisir des unités cohérentes pour les mesures et d’utiliser une valeur précise de π pour des résultats plus précis. La connaissance du volume d’un ellipsoïde peut être précieuse dans divers domaines de l’étude et de la pratique.