
Volume d’un cône de révolution : Calculateur en ligne, définition et exemples de calcul
Calculateur du volume d’un cône de révolution
Définition d’un cône de révolution
Un cône de révolution est un solide engendré par la rotation d’un triangle rectangle autour d’un des côtés de l’angle droit.
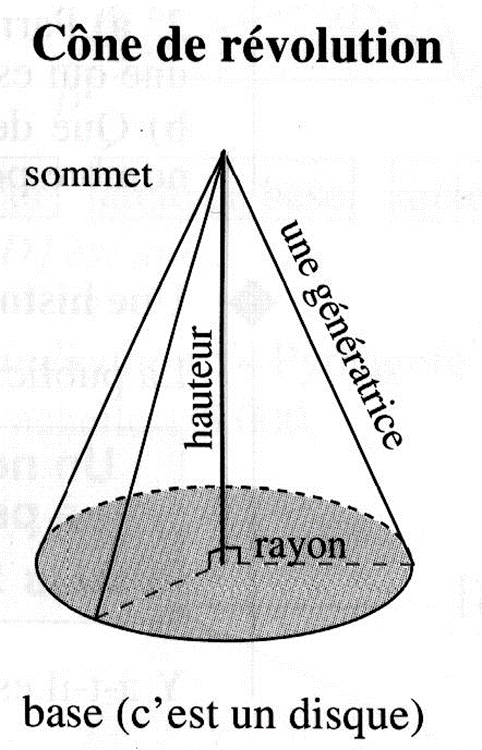
Un cône de_révolution est formé :
- d’un disque appelé base
- d’une surface courbe appelée face latérale
- d’un point appelé sommet du cône
Hauteur d’un cône de révolution
La hauteur d’un cône est le segment joignant son sommet au centre de la base.
On appelle aussi hauteur la longueur de ce segment.
Comment calculer le volume du cône ?
Le volume V d’un cône de rayon r est égal au tiers de l’aire de la base fois la hauteur. Le volume d’un cône est inférieur à celui d’un cylindre de même base et de même hauteur. En fait, c’est exactement le tiers du volume du cylindre. La formule est :
Volume =1/3 × Aire de la base × hauteur
Avec l’aire de la base du conne de_révolution est égale à πR2
D’où
Volume = ( πR2 .h)/3
Exemple de calcul du volume d’un cône de révolution
Exemple 1
Calculer le volume du cône dont la base est un disque de rayon 3cm et dont la hauteur est égale à 5cm
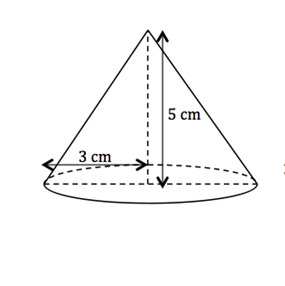
Solution
Aire (base) = π×32 = 28.27 cm2
Volume = ( 28.27 × 5)/3 = 47.12 cm3
Exemple 2
Un cornet de glace a la forme d’un cône de hauteur SO = 10 cm, de rayon de disque de base OA = 3 cm.
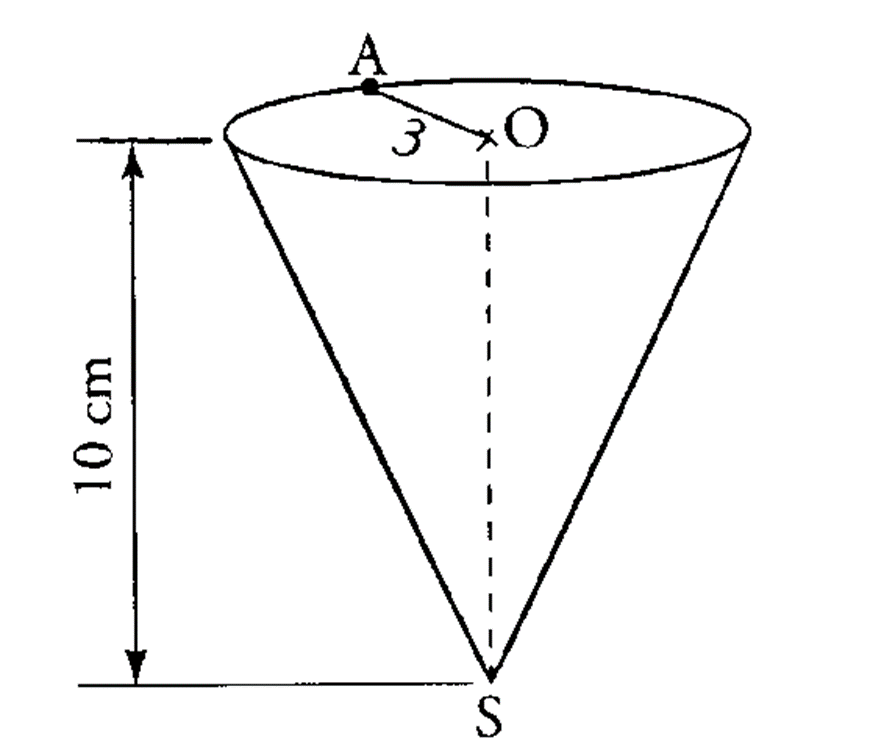
Calculer le volume exact de glace contenue dans le cône.
Solution :
Solution :
volume du cône = ( πR2 .h)/3
volume du cône = ( π×32 × 10)/3
volume du cône = ( 90.π)/3
D’où le exact de glace contenue dans le cône est 94.25 cm3
Exemple 3
Un paysan chinois doit transporter de l’eau pour arroser une petite parcelle de terre.
Son seau étant percé, il utilise comme récipient son chapeau en forme de cône de_révolution dont la base est un disque de rayon 25 cm et dont la hauteur mesure 30 cm.

Quelle quantité d’eau peut-il transporter ?
Solution :
V = ( πR2 .h)/3
V = ( π × 252 × 30)/3 ≈ 19 635 cm3 ≈ 19,6 L
Avec son chapeau, il peut transporter environ 19,6 L d’eau.









