
Loi d’Ohm : Calcul en ligne, Définitions, Énoncé, Utilisation de la loi d’ohm et exercices corrigés
Calculateur de la loi d’ohm
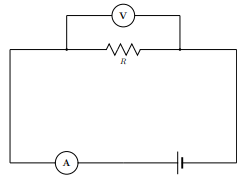
Qu’est-ce que la loi d’ohm ?
La loi d’ohm établit une relation entre la valeur d’une résistance, la tension qu’elle reçoit et l’intensité du courant qui circule.
Définitions
La résistance électrique
- La résistance électrique est la propriété des conducteurs électriques de s’opposer au passage des électrons.
- La résistance électrique dépend de la nature et des dimensions du conducteur. La résistance d’un conducteur de matériau donné est d’autant plus élevée que la longueur du conducteur est élevée et que son diamètre est petit.
- Symbole de la résistance électrique : R
- Unité SI de la résistance : Ω (Ohm)
Le courant électrique
Le courant électrique correspond au déplacement d’électrons « enlevés » à des atomes que l on a de ce fait chargé électriquement. On appelle ces électrons des électrons libres. Ils se déplacent dans un milieu dit conducteur formant un circuit électrique.
Intensité du courant électrique
Si on pouvait observer un point quelconque d’un circuit électrique en fonctionnement et y compter le nombre d’électrons passant pendant un temps donné, on mesurerait alors le « débit » d’électrons libres. Ce « débit d’électrons» est appelé intensité du courant électrique.
Le courant est désigné par la lettre I, il se mesure en Ampère [A].
Un courant de 1[A] (un ampère) correspond au passage de « beaucoup » d’électron (6,25×1018 électrons ).
La tension électrique
Le courant électrique est un déplacement d’électrons et le débit de ces électrons permet de définir l’intensité du courant. Mais, pour qu’il y ait circulation des électrons il faut disposer d’un générateur de courant dont la caractéristique sera de créer un déséquilibre de charge, capable « d’attirer et de repousser » les électrons. Ce déséquilibre de charge sera appelé tension électrique.
Autrement dit, la présence d un générateur aux bornes d un circuit conducteur permet la création d une tension qui « entraîne » la mise en mouvement des électrons. Le courant électrique généré pourra être utilisé pour faire fonctionner un appareil que l on appellera récepteur
Énoncé de la loi d’ohm
La tension U aux bornes d’un récepteur de résistance R et parcouru par un courant I est donnée par une formule dite « Loi D’OHM » qui s’écrit :
U = R x I

On note :
- U : la tension aux bornes de la résistance.
- I : l’intensité du courant qui circule à travers la résistance
- R : la valeur de la résistance.
Remarque :
Pour que la loi d’ohm soit respectée la tension doit être exprimée en volt (V), l’intensité en ampère (I) et la résistance en ohm (Ω)
Utilisation de la loi d’ohm
Selon son expression et les grandeurs connues la loi d’ohm permet d’obtenir différentes grandeurs :
- Sous la forme U = R x I elle permet de calculer le tension lorsque la résistance et l’intensité sont connues.
- Sous la forme I = U / R elle permet de calculer l’intensité lorsque la tension et la résistance sont connues.
- Sous la forme R = U / I elle permet de calculer la résistance lorsque la tension et l’intensité sont connues.
Exercices corrigés sur la loi d’Ohm:
Exercice 1 :
La tension aux bornes d’un dipôle passif linéaire est U = 4,2 V . Ce dipôle est traversé par un courant d’intensité I = 70 mA.
Calculer la valeur de la résistance R de ce dipôle.
Solution :
Pour calculer la résistance R du dipôle, on applique la relation R=U/I
Application numérique : R= 4.2 / 0.07 avec 70 mA = 0.07 A
D’où R = 60 Ω
Exercice 2 :
Un dipôle ohmique de résistance 3300 Ω est détérioré si l’intensité du courant qui le traverse est supérieure à 25 mA.
Quelle tension maximale peut-on appliquer entre les bornes du dipôle sans le détériorer ?
Solution :
Ici, R = 3300 Ω et Imax = 25 mA
Conversion : Imax = 0,025 A
Umax = R x Imax = 3300 x 0,025 = 82,5 V.











