Volume d’un tore : Calculateur, définition, formule et exemple de calcul
Calculateur du volume d’un tore
Définition du tore
Un tore est une forme géométrique tridimensionnelle qui ressemble à un anneau ou à un beignet. Il est créé en faisant tourner un cercle autour d’un axe qui ne le traverse pas. Le résultat est une surface courbe qui forme une boucle continue tout au long de sa circonférence.
Plus précisément, un tore est défini par deux rayons : le rayon du cercle central (R) et le rayon de la section transversale (r). Le rayon du cercle central est la distance du centre du tore au centre du tube qui forme le tore. Le rayon de la section transversale est la distance du centre du tube jusqu’à la surface extérieure du tore.
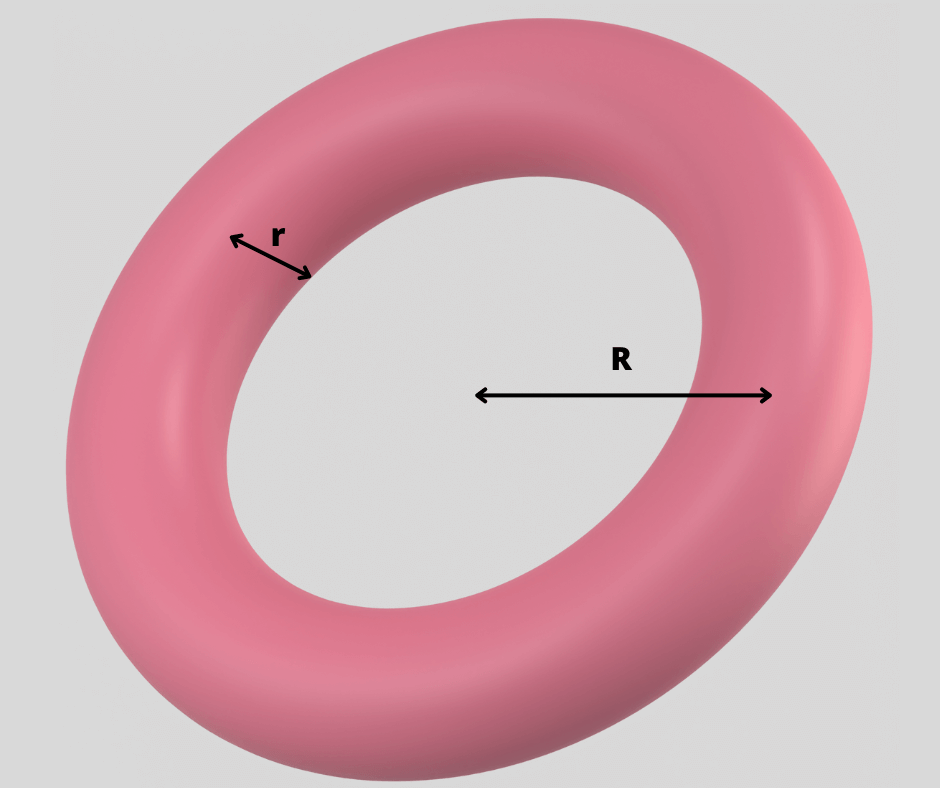
Le tore possède des propriétés intéressantes, telles que sa symétrie axiale et son absence de bords. Il est utilisé dans divers domaines, tels que la géométrie, la physique et l’architecture, en raison de sa forme distinctive.
Il est important de noter que le terme “tore” est parfois utilisé de manière plus générale pour désigner toute forme annulaire, même si elle ne respecte pas strictement les définitions géométriques précises.
Formule pour le calcul du volume d’un tore
La formule générale pour calculer le volume d’un tore est la suivante :
V = 2π² × R × r²
Dans cette formule, V représente le volume du tore, π est une constante approximativement égale à 3,14159, R est le rayon du cercle central du tore (également appelé le grand rayon), et r est le rayon de la section transversale du tore (également appelé le petit rayon).
Le volume d’un tore dépend à la fois du rayon du cercle central (R) et du rayon de la section transversale (r). Plus ces rayons sont grands, plus le volume du tore sera important.
Procédure pour calculer le volume d’un tore
Suivez attentivement ces étapes pour calculer le volume d’un tore :
Étape 1 : Mesurez les rayons
Prenez un instrument de mesure, tel qu’une règle ou un mètre, et mesurez le rayon du cercle central du tore (R). Assurez-vous de mesurer à partir du centre du tore jusqu’à la surface du cercle central. Notez cette valeur.
Ensuite, mesurez le rayon de la section transversale du tore (r). Cela peut être réalisé en mesurant la distance du centre du tore jusqu’à la surface extérieure du tore dans une direction perpendiculaire au cercle central. Notez également cette valeur.
Étape 2 : Élevez le rayon de la section transversale au carré
Prenez la valeur du rayon de la section transversale (r) que vous avez mesurée et élevez-la au carré. Cela signifie simplement la multiplier par elle-même.
(r² = r × r)
Étape 3 : Appliquez la formule pour calculer le volume
Prenez la formule V = 2π² × R × r² et remplacez les valeurs mesurées de R et r par celles que vous avez notées dans les étapes précédentes.
Effectuez les calculs nécessaires en multipliant 2π² par R et par r² pour obtenir le volume du tore.
Étape 4 : Obtenez le résultat
Une fois que vous avez effectué les calculs, vous obtiendrez le volume du tore en unités cubiques, correspondant à l’unité de longueur que vous avez utilisée pour mesurer les rayons.
Exemple de calcul du volume d’un tore
Prenons un exemple pour illustrer le calcul du volume d’un tore :
Supposons que nous ayons un tore avec un rayon du cercle central (R) de 7 cm et un rayon de la section transversale (r) de 3 cm. Appliquons la formule pour calculer le volume du tore :
V = 2×π² × R × r²
V = 2×3.14159² × 7 cm × (3 cm)²
V ≈ 1243.57 cm³
Ainsi, le volume du tore est d’environ 1243.57 cm³.
Conclusion
Calculer le volume d’un tore peut sembler complexe au premier abord, mais en suivant les étapes appropriées, il devient un processus réalisable. En utilisant la formule V = 2π² × R × r² et en mesurant correctement les rayons du tore, vous pouvez obtenir le volume souhaité.