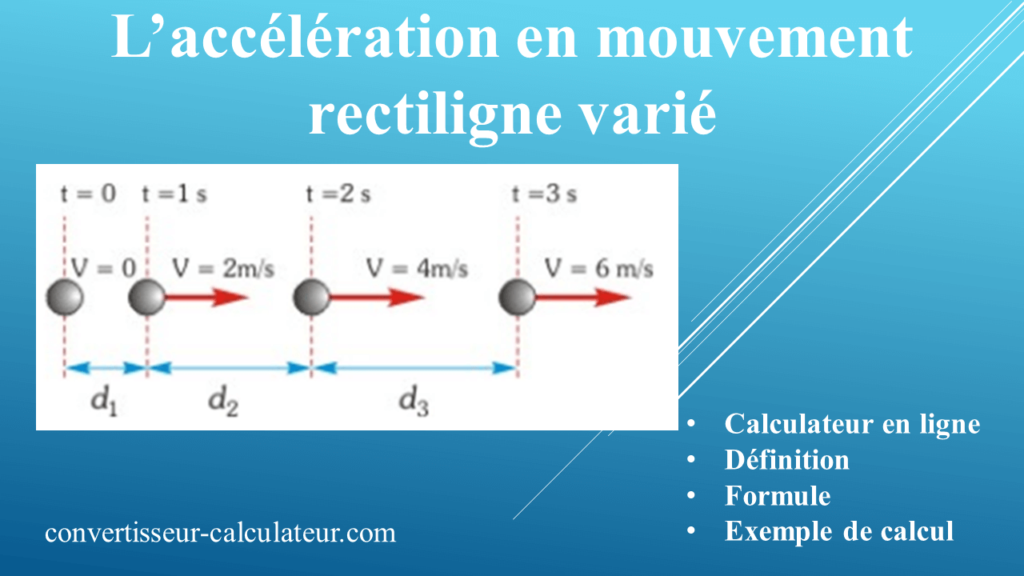
Accélération en mouvement rectiligne varié : Calculateur en ligne, définition, formule et exemple de calcul
Calculateur de l’accélération en mouvement rectiligne varié
Définition
Le mouvement rectiligne uniformément varié est le mouvement caractérisé par une trajectoire rectiligne parcourue à une vitesse qui varie proportionnellement avec le temps.
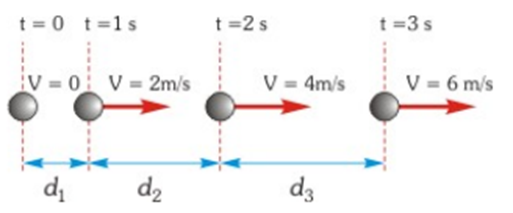
- Le mouvement sera accéléré MRUA si la vitesse augmente proportionnellement en fonction du temps
- Le mouvement sera décéléré MRUD si la vitesse diminue proportionnellement en fonction du temps
Dans notre vie quotidienne, nous parlons d’accélération (augmentation de vitesse) et de décélération (diminution de vitesse) mais sans les mesurer. La mesure de cette grandeur se fait par référence au temps (comme la vitesse).
Comment calculer l’accélération moyenne d’un mouvement rectiligne ?
Lorsque la vitesse d’un mobile n’est plus constante, l’accélération est la grandeur physique qui caractérise la variation de la vitesse au cours du temps.
L’accélération moyenne d’un objet est donc donnée par la relation suivante :
amoyenne = (Vf-Vi)/(tf-ti)= ∆V / ∆t
Avec
- V : la vitesse en m.s-1.
- t : le temps en s.
- a : l’accélération en m.s-2.
Exemple de calcul de l’accélération en mouvements rectiligne varié
Une voiture initialement en mouvement avec la vitesse de 120 km/h, freine avec accélération constante de sorte qu’elle arrive au repos au bout de 5 s.
Quelle est l’accélération du mouvement ?
Réponse :
Afin de résoudre cet exercice, il faut obligatoirement faire un croquis en y reportant toutes les données.
Choisissons l’origine des espaces telle qu’elle coïncide avec la position du de la voiture à t0 = 0 : x0 = 0.
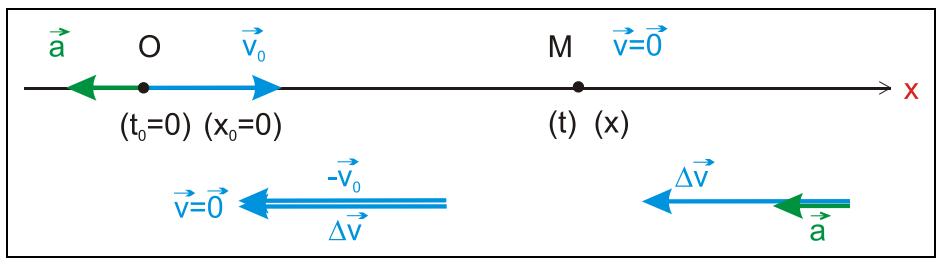
L’accélération est donnée par :
amoyenne = (Vx-Vx0)/(tx-t0)= ∆V / ∆t
avec vx = 0 , vx0 = (120 / 3,6)=33.33m/s et t = 5 s
Donc :
amoyenne = (0-33.33)/(5-0)
amoyenne = -6.6 m.s-2
ax < 0 signifie que l’accélération est orientée dans le sens opposé à celui de l’axe Ox.









