Aire d’un triangle -Calcul en ligne

Aire d’un triangle : Calculateur, définition et exemple de calcul

Calculateur d’aire du triangle en ligne

Définition du triangle

• Le triangle est une forme géométrique composée de trois angles et trois côtés.
• Les valeurs des angles et des côtés peuvent varier sur certains triangles.
• Les angles sont aussi nommés « sommets » du triangle.
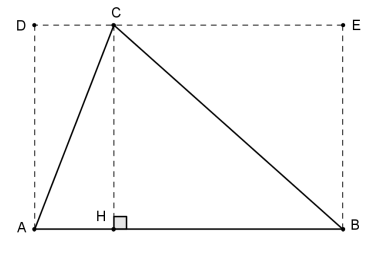
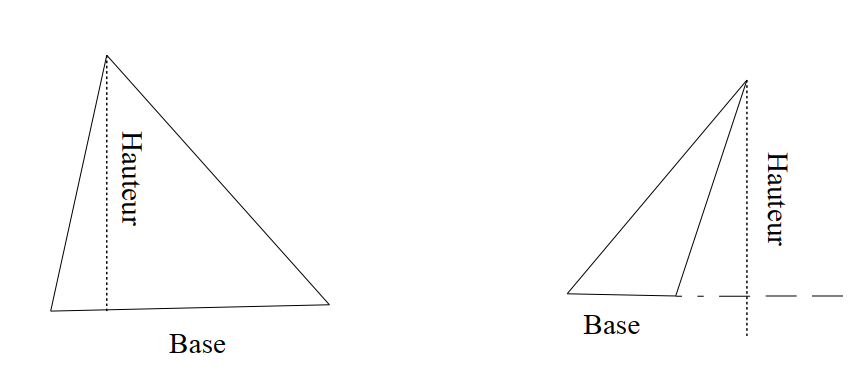
• Un triangle peut être considéré comme un « demi-rectangle ». En effet, la hauteur [CH] issue de C du triangle (ABC) a même mesure que les largeurs [AD] et [BE] du rectangle (ABCD). Les triangles (AHC) et (ADC) sont symétriques par rapport au milieu de [AC] et sont ainsi de même aire. De même pour (BCH) et (BCE)

Le triangle isocèle

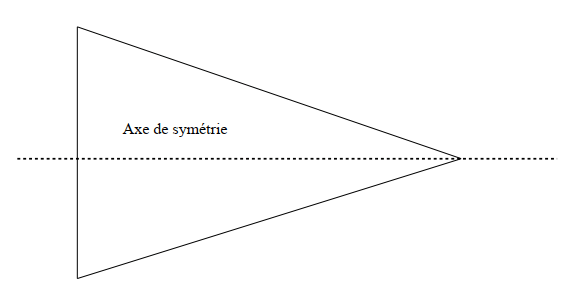
Le terme isocèle veut dire qu’il a 2 côtés identiques

Les particularités du triangle isocèle :

• Il est reconnaissable par le fait qu’il possède 2 angles de même valeur
• Il est aussi doté de 2 cotés identiques
• Il possède un seul axe de symétrie.

Le triangle équilatéral

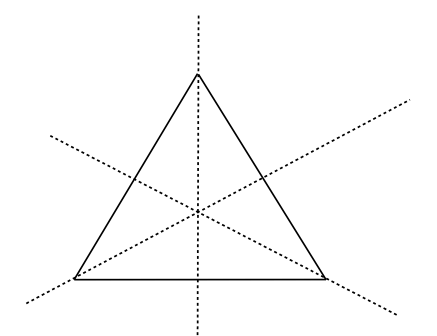
Le terme équilatéral veut dire « des côtés de mêmes longueurs ».

Les particularités du triangle équilatéral :

• Les 3 angles sont de même valeur et représentent toujours 60°
• Les 3 cotés sont identiques dans leur longueur
• Le triangle équilatéral possède 3 axes de symétrie

Le triangle rectangle

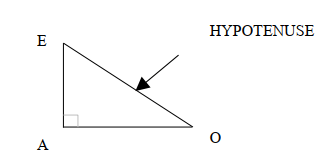
• Le triangle rectangle est une forme qui comporte trois sommets EAO
• Il comporte un angle à 90°(A). On peut dire que cet angle est la somme de l’addition des deux autres angles.
• Le triangle rectangle est simplement le résultat d’un rectangle coupé en deux parties par la diagonale.
• Le triangle rectangle possède un coté plus grand que les deux autres. Ce grand coté s’appelle HYPOTENUSE.
• Ce côté « Hypoténuse » a été objet du théorème de Pythagore.

Comment calculer l’aire d’un triangle ?

Pour calculer l’aire des triangles quelconques, isocèles et équilatéraux, triangle rectangle … on applique la formule mathématique de l’aire d’un triangle :

Aire = (Base  × hauteur) / 2

La hauteur est toujours perpendiculaire à la base

Exemple° 1 sur le calcul d’aire d’un rectangle

Un triangle a une base de 7 cm et une hauteur de 4 cm.

Quelle est l’aire de ce triangle ?

Réponse :

Pour résoudre ce problème, On doit appliquer la formule mathématique du calcul de l’aire d’un triangle :

• A = (Base × hauteur) / 2
• A = (7 × 4) / 2
• A = 28 / 2
• A = 14 cm²

L’aire de ce triangle est de 14 cm².

Exemple N°2 sur le calcul d’aire d’un rectangle

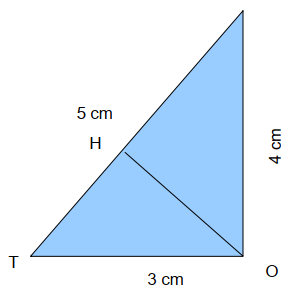
Réponds aux questions suivantes sans faire de dessin.

a. Quelle est l’aire du triangle rectangle(LOT)

b. Que cherches tu en calculant (OH x LT) / 2

c. Déduis en la longueur [OH]

Réponse :

a. Aire_LOT= (4×3)/2= 6cm²

b. On cherche alors l’aire du triangle (LOT).

c.  On a (OH x LT) / 2 = 6

Donc OH x LT = 12

Donc OH = 12 : LT

C’est à dire OH = 12:5 = 2,4 cm

Voir aussi :

Autres sujets peuvent vous intéresser