Volume d’une boule : Définition, calcul en ligne, formule et exemples de calcul
Calculateur du volume d’une boule
Définition d’une sphère et boule
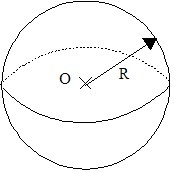
La sphère de centre O et de rayon R est l’ensemble des points de l’espace dont la distance à O est égale à R.

La boule de centre O et de rayon R est l’ensemble des points de l’espace dont la distance à O est inférieure ou égale à R.
Remarque
- Un diamètre de la sphère est un segment qui joint deux points de la sphère et qui passe par son centre O.
- Toute droite passant par le centre d’une sphère coupe celle-ci en deux points diamétralement opposés.
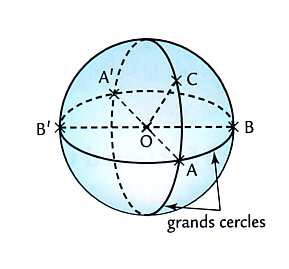
- Un cercle de centre O et de rayon R s’appelle un grand cercle de la sphère.
Exemple :
Les points appartenant à une sphère sont représentés sur des cercles de la sphère de centre O appelés grands cercles. [OB] et [OC] sont deux rayons de la sphère, donc OB = OC.
Comment calculer le volume d’une boule?
le volume d’une boule de rayon R est donnée par la relation suivante :
V=\frac{4}{3}\pi R^{3}Exemple de calcul du volume d’une_boule.
Exemple N°1 :
Calculer le volume d’une_boule de rayon 2m.
Solution :
le volume de la boule est égale à :
V=\frac{4}{3}.\pi .R^{3}= \frac{4}{3}.\pi .2^{3}D’où V= 33.49 m3
Exemple N°2 :
Un ballon de football à un diamètre de 24cm. Calculer son volume.
Solution
le volume du ballon est égale à :
V=\frac{4}{3}\pi R^{3}= \frac{4}{3}.\pi .24^{3}D’où V= 57,876.48 cm3= 0.05787648 m3










