Triangle rectangle – calcul des angles et des longueurs : Calculateur en ligne, Formules et exemple de calcul
Calculateur triangle rectangle
Cosinus d’un angle aigu
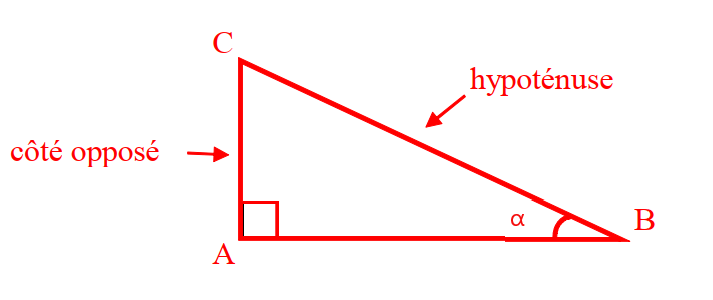
Soit ABC un triangle rectangle en A. On appelle cosinus de l’angle α, le quotient de la longueur du côté adjacent à l’angle α par la longueur de l’hypoténuse.

Cos α = coté adjacent /hypoténuse = AB /BC
Sinus d’un angle aigu
Soit ABC un triangle rectangle en A. On appelle sinus de l’angle α, le quotient de la longueur du côté opposé à l’angle α par la longueur de l’hypoténuse.
Cos α = coté adjacent /hypoténuse = AC /BC
Tangente d’un angle aigu
Soit ABC un triangle rectangle en A. On appelle tangente de l’angle α, le quotient de la longueur du côté opposé à l’angle α par la longueur du côté adjacent à l’angle α.
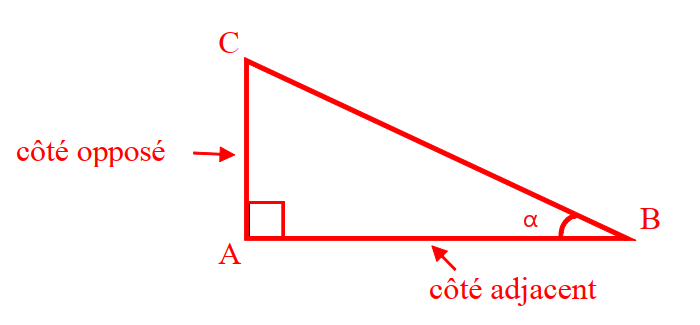
Tan α= côté opposé / côté adjacent = AC / AB
Application au calcul de longueur d’un côté du triangle rectangle
Pour calculer la longueur d’un côté du triangle rectangle, il faut connaitre une longueur et la mesure d’un angle.
Exemple 1 :
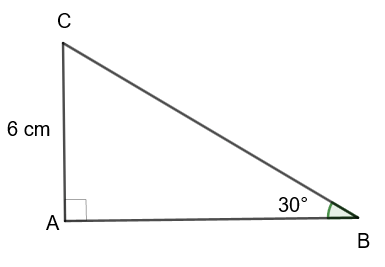
Calculer la valeur du côté AB dans le triangle ci-dessous :
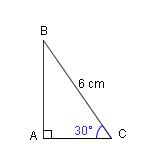
On connaît la longueur de l’hypoténuse et on cherche la longueur du côté opposé à l’angle donné. On applique donc la formule du sinus.
Dans le triangle ABC rectangle en A on a : 𝑠𝑖𝑛 30° = AB/6
Donc AB = 6 × sin 30° = 6 × 0,5 = 3 cm
D’où AB = 3 cm
On vérifie bien la cohérence des résultats: On recherche le côté opposé à un angle qui doit être de longueur inférieur à la longueur de l’hypoténuse et on a bien 3 < 6.
Exemple 2 :
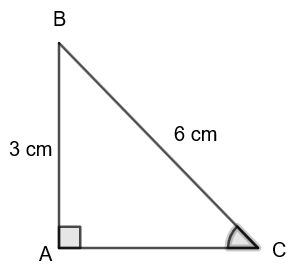
Calculer la valeur du côté CB dans le triangle ci-dessous :
On connaît la longueur du côté opposé à l’angle donné et on cherche la longueur de l’hypoténuse. On applique donc la formule du sinus.
Dans le triangle ABC rectangle en A on a : 𝑠𝑖𝑛 (30° ) = 6 / BC
Donc BC = 6 / 𝑠𝑖𝑛 (30°) = 6/0.5
BC = 6/0.5
D’où BC = 12 cm
On vérifie bien la cohérence des résultats: On recherche la longueur de l’hypoténuse qui est le côté le plus grand et on a bien 12 > 6.
Application au calcul de la mesure d’un angle
Pour cela il faut connaitre la longueur de deux côtés pour trouver la mesure d’un angle.
Exemple : Dans le triangle ci-dessous calculer l’angle α.
On connaît la longueur de l’hypoténuse et la longueur du côté opposé à l’angle cherché. On applique donc la formule du sinus.
Dans le triangle ABC rectangle en A on a : 𝑠𝑖𝑛 α = 𝐴𝐵 / 𝐵𝐶
𝑠𝑖𝑛 α = 3/6 = 0,5. On a donc α = 30°.
Voir aussi :
Autres sujets peuvent vous intéresser
Calcul de longueur ou d’angle dans un triangle rectangle : Calculateur en ligne, Formules et exemple de calcul
Calcul de longueur ou d’angle dans un triangle rectangle : Calculateur en ligne, Formules et exemple de calcul
Calcul de longueur ou d’angle dans un triangle rectangle : Calculateur en ligne, Formules et exemple de calcul









