
L’ellipse : calcul d’aire en ligne, définition, propriétés, formule et exemple de calcul
Calculateur d’aire d’une ellipse
Définition
Une ellipse est l’ensemble des points du plan dont la somme des distances à deux points fixes F et F’ est une constante supérieure à FF’. Voir figure ci-dessous :
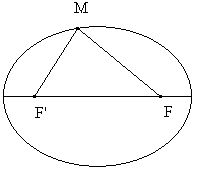
Les points F et F’ sont appelés les foyers de (E).
Propriétés
- Toute ellipse de foyers distincts F et F’ admet deux axes de symétrie et un point de symétrie.
- Les deux axes sont la droite (FF’) et la médiatrice du segment [FF’].
- Le centre de symétrie est le milieu de [FF’]
- La droite (FF’) est l’axe focal de (E).
- Le réel positif FF’ = 2 c est la distance focale.
- La médiatrice du segment [FF’] est l’axe non focal de (E).
- Le réel positif AA’ = 2 a est le grand axe de (E).
- Le réel positif BB’ = 2 b est le petit axe de (E).
- Les points A, A’, B et B’ sont les sommets de (E)
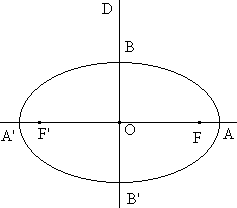
Comment calculer l’aire d’une ellipse ?
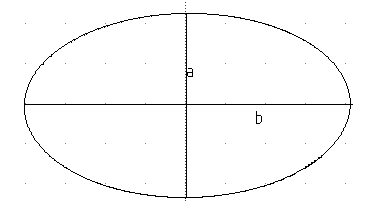
Pour calculer l’aire d’une ellipse on utilise la formule suivante :
Aellipse = 𝜋 × 𝑎 × 𝑏
Avec :
- a : demi-petit axe
- b : demi-grand axe
Exemple de calcul
Calcul de la surface d’une ellipse connaissant la longueur des deux axes.
Le grand axe vaut 35 cm et le petit axe est égal à 25 cm.
- a = 25 cm /2 = 12.5 cm
- b =35 cm / 2 = 17.5 cm
Donc,
Aellipse = 𝜋 × 𝑎 × 𝑏
Aellipse = 𝜋 × 17.5 × 12.5
Aellipse = 687.22









