Aire d un disque : définition, formule , calcul en ligne et exemple d’application
Calcul en ligne
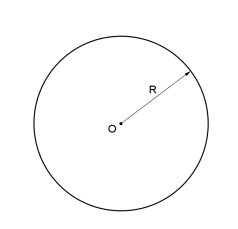
Définition
- Le cercle de centre O et de rayon R est l’ensemble des points situés à la distance R du point O.
- On appelle rayon le segment qui joint un point du cercle au centre du cercle.
- On appelle diamètre le segment qui joint deux points du cercle en passant par le centre du cercle.
- On appelle corde le segment qui joint deux points du cercle.
- On appelle arc de cercle une partie d’un cercle.
Comment calculer l’aire d’un disque?
L’Aire d’un disque (A) est égale au produit du nombre pi (π) par la longueur du rayon R du cercle au carré :
Aire d’un disque = π x R²
Exemple de calcul d’aire d’un_disque
Soit un cercle de centre O et de rayon R. Sachant que la longueur de R = 5 m, son aire sera égale à :
Aire A = π x R² = 3,14 x 5² = 3,14 x 9 = 78.5 m²
Attention aux unités de mesure des aires : cm², m², km²…










