Théorème d’Al-Kashi – loi des cosinus dans un triangle : Définition, calculateur en ligne, Formules et démonstration
Calculateur de la loi des cosinus
Théorème d’Al-Kashi – loi des cosinus
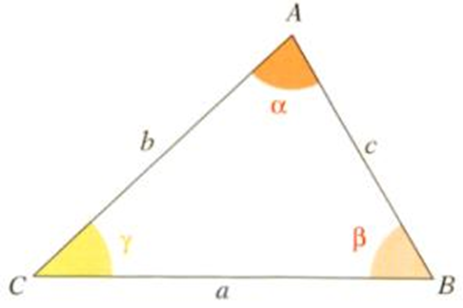
Dans un triangle ABC on a :
a2= b2+c2– 2×b×c×cos(α)
b2= a2+c2– 2×a×c×cos(β)
c2= a2+b2– 2×a×b×cos(𝛾)
Le théorème d’Al-Kashi est également connu sous le nom de théorème de Pythagore généralisé, car le théorème de Pythagore en est un cas particulier : lorsque l’angle α est droit, autrement dit lorsque cos α = 0, le théorème d’Al-Kashi s’écrit : a2 = b2 + c2.
Démonstration du théorème d’Al-Kashi – loi des cosinus
Considérons le triangle suivant :
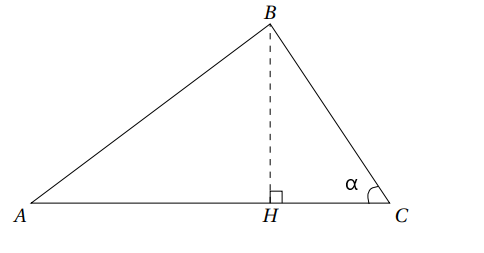
Etape 1 :
Dans le triangle HBC on a CH = BC×cos(α) donc AH = AC-BC×cos(α). De même on a BH = BC×sin(α) . On a donc le dessin suivant :
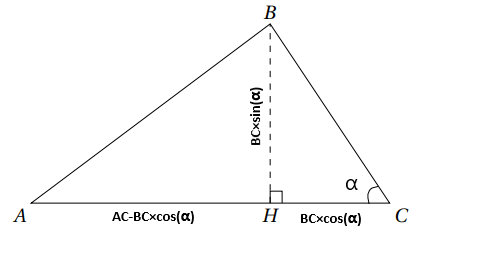
Etape 2 :
De plus, d’après le théorème de Pythagore dans le triangle ABH on a : AB2 = AH2 + BH2.
Et donc, d’après l’étape précédente :
AB2 = (AC-BC×cos(α))2 + (BC×sin(α))2
Etape 3 :
Ce qui donne, après avoir développé : AB2 = AC2-2× AC× BC×cos(α) + BC2×cos(α) 2+ BC2×sin(α)2.
En factorisant BC2 on a : AB2 = AC2+ BC2(cos(α) 2+ sin(α)2)-2× AC× BC×cos(α)
Et puisque cos(α) 2+ sin(α)2=1
on a :
AB2 = AC2+ BC2-2× AC× BC×cos(α)
C’est exactement le théorème que l’on voulait démontrer









