Résistance équivalente, résistances en parallèle et en série : Calculateur en ligne, Définition, Formules et exercices corrigés
Calculateur de la résistance équivalente (résistances en parallèle et en série)
La résistance électrique traduit la propriété d’un matériau à s’opposer au passage d’un courant électrique. Elle est souvent désignée par la lettre R et son unité de mesure est l’Ohm. Elle est liée aux notions de résistivité et de conductivité électrique.
Symbole : Ω.
Différents types de montage des résistances
Montage des résistances en série
On dit que deux ou plusieurs résistances sont branchées en série lorsqu’elles sont reliées l’une à l’autre bout à bout par un conducteur, de telle sorte à former un seul conducteur dans lequel un même courant peut passer.
Calcul de la résistance équivalente
La résistance équivalente à plusieurs résistances associées en série est égale à la somme des résistances.
Réq = R1 + R2 + … + Rn
Démonstration
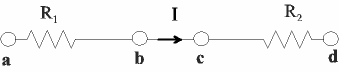
La différence de potentiel aux bornes de R1 vaut :
∆V1 = Va – Vb = R1 × I,
De même, aux bornes de R2 :
∆V2 = Vc – Vd = R2 × I,
La différence de potentiel aux bornes de l’ensemble formé par les deux résistances en série vaut :
∆V = Va – Vd = Va – Vb + Vb – Vd = Va – Vb + Vc – Vd .
En effet, puisque la résistance du fil conducteur qui lie b à c est négligeable, Vb– Vc ≈ 0 × I ≈ 0 et Vb = Vc. Dès lors, en vertu des relations précédentes :
∆V = ∆V1 + ∆V2 = R1 × I + R2 × I = (R1 + R2) × I
Donc, la différence de potentiel aux bornes de deux résistances placées en série est égale à la somme des différences de potentiel aux bornes de chacune des résistances
L’ensemble formé par les résistances R1 et R2 en série, offre donc au passage du courant une résistance équivalente :
Réq = ∆V/I = R1 + R2.
Montage des résistances en parallèle
On dit que deux ou plusieurs résistances sont branchées en parallèle, lorsqu’elles sont groupées ont leurs deux extrémités connectées ensembles au reste du circuit.
Calcul de la résistance équivalente
L’inverse de la résistance équivalente 𝑅𝑒q est égale à la somme des inverses des résistances montés en parallèle.
1 /𝑅éq = 1 /𝑅1 + 1 /𝑅2 + 1 /𝑅3 + …. + 1 /𝑅n
Démonstration
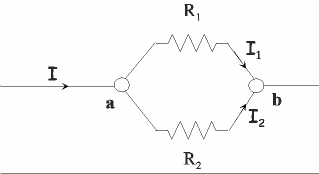
La différence de potentiel aux bornes de l’ensemble est égale à celle aux bornes de chaque résistance placée en parallèle.
∆V = Va – Vb = ∆V1 = ∆V2
Par contre, le courant total I se divise lorsqu’il arrive en a, une partie, I1, passant par R1, l’autre, I2, passant par R2 :
I = I1 + I2 (1)
La résistance équivalente offerte au passage du courant par l’ensemble des deux résistances en parallèle est donnée par :
Réq = ∆V/I, donc I = ∆V/ Réq (2)
On remplace (2) dans (1) donc :
∆V/𝑅éq = ∆V/𝑅1 + ∆V/𝑅2
En divisant membre à membre par ∆V, il vient :
1/𝑅éq = 1/𝑅1 + 1/𝑅2
Remarques :
- Lors d’une association en parallèle, la résistance Rep est plus petite que la plus petite des résistances.
- Pour deux résistances R1 et R2 en parallèle, on a : Rep =(R1 × R2)/ (R1 + R2) = Produit /Somme. Attention cette formule est valable uniquement pour deux résistances.
Exercices corrigés sur le calcul de la résistance équivalente (résistances en parallèle et en série)
Exercice 1 :
Calculer la résistance équivalente du montage ci-dessous :
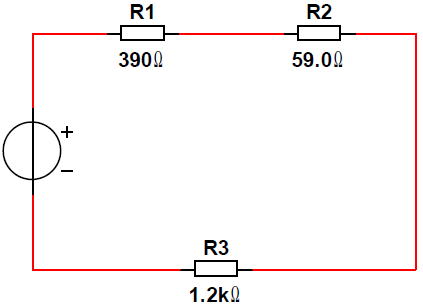
Req = R1 + R2 + R3 = 390 + 59 + 1200 = 1649 Ω
D’où, Req = 1,649 kΩ
Exercice 2 :
Calculer la résistance équivalente du montage ci-dessous :
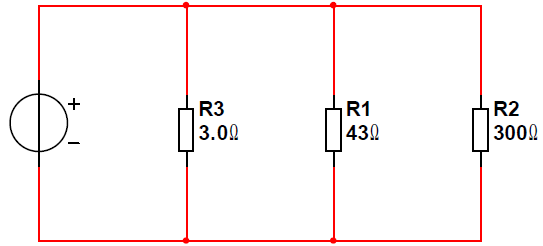
1/Req= 1/R1+1/R2+1/R3 =1/43 +1/300+1/3 = 0,3599
D’où, Req= 1/0,3599 = 2,77 Ω
Exercice 3 :
Calculer la résistance équivalente du circuit ci –dessous :
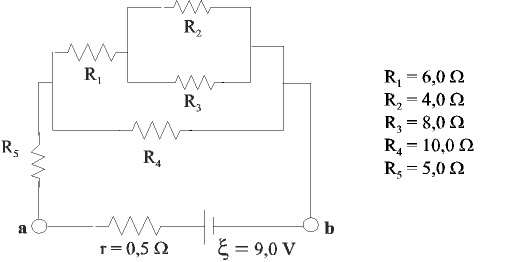
Les résistances R2 et R3 placées en parallèle ont une résistance équivalente R23, donnée par :
1/R23 = 1/𝑅2 + 1/𝑅3
R23 = 2.7 Ω
Ce système se trouve groupé en série avec la résistance R1, ce qui donne pour la résistance équivalente de la branche supérieure du circuit :
R123 = R1 + R23 = 6.0 + 2.7 = 8.7 Ω.
Cette résistance de la branche supérieure est placée en parallèle avec R4, ce qui donne en les combinant :
1/R1234 = 1/𝑅123 + 1/𝑅4
R1234 = 4.8 Ω
Pour obtenir la résistance équivalente de tout le circuit branché aux bornes (a) et (b) de la pile, il faut encore lui ajouter R5, branchée en série :
Réq = R1234 + R5 = 4.8 + 5.0 = 9.8 Ω.
Réq = 9.8 Ω.
Voir aussi :
Autres sujets peuvent vous intéresser
Résistance équivalente, résistances en parallèle et en série : Calculateur en ligne, Définition, Formules et exercices corrigés
Résistance équivalente, résistances en parallèle et en série : Calculateur en ligne, Définition, Formules et exercices corrigés
Résistance équivalente, résistances en parallèle et en série : Calculateur en ligne, Définition, Formules et exercices corrigés
Résistance équivalente, résistances en parallèle et en série : Calculateur en ligne, Définition, Formules et exercices corrigés
Résistance équivalente, résistances en parallèle et en série : Calculateur en ligne, Définition, Formules et exercices corrigés