Pont diviseur de tension : Calcul en ligne, définition, formules et exercices corrigés
Calculateur du pont diviseur de tension
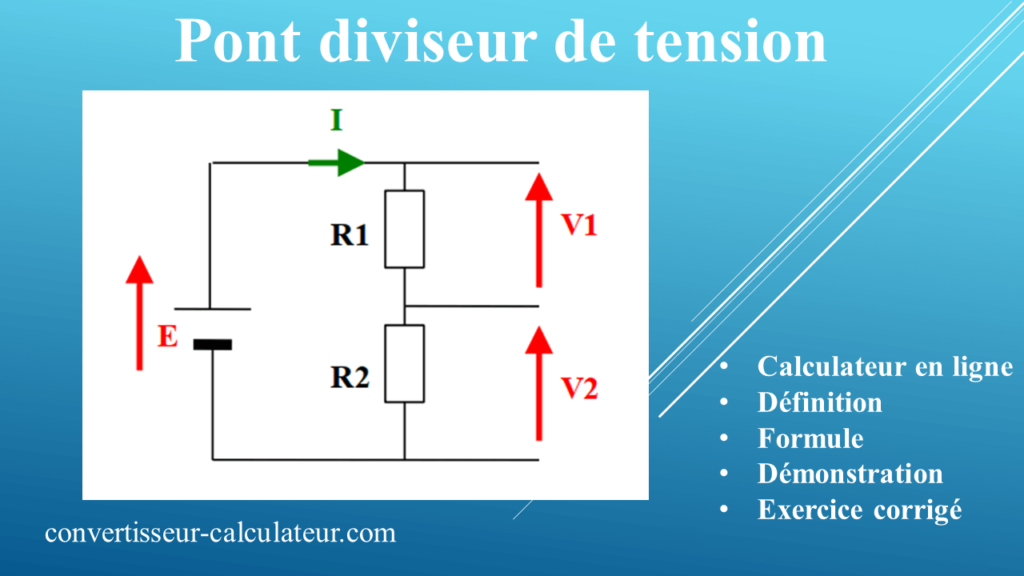
Pont diviseur de tension
Le pont diviseur de tension est un montage électrique simple. Il permet de déterminer une tension proportionnellement à une autre tension. Ce type de montage est utilisé couramment pour créer une tension de référence dans un circuit électrique.
Théorème
Dans un montage pont diviseur de tension, la tension de sortie aux bornes d’un des résistors est égale au produit de la tension d’entrée multipliée par la valeur du résistor ou est mesurée cette tension et divisée par la somme des valeurs des deux résistors du montage.
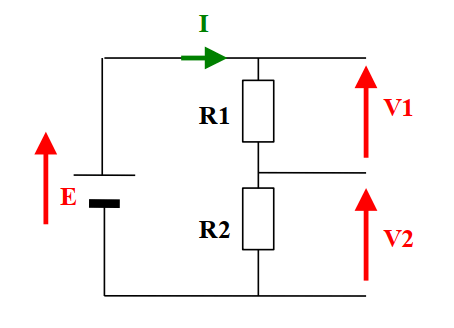
V1 = E * (R1/ (R1+R2))
V2 = E * (R2/ (R1+R2))
Démonstration
La plus simple représentation du diviseur de tension consiste à placer deux résistances électriques en série (voir le schéma ci-dessous). Ce type d’association de résistances étant omniprésent dans les montages électriques, le pont diviseur en devient une des notions fondamentales en électronique.
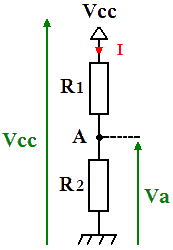
Il est possible de calculer facilement la valeur de Va dans le montage ci-dessus, à la condition de connaitre les valeurs des résistances et la valeur de la tension Vcc. La première formule à utiliser est celle de la loi d’Ohm qui permet de citer cette équation :
I = Vcc / (R1+R2)
En utilisant la loi d’Ohm une seconde fois, il est possible de déterminer l’équation suivante :
Va = R2 × I
Dans la formule ci-dessous, il suffit de remplacer le courant (I) par sa valeur équivalente pour déterminer facilement l’équation de Va :
Va = Vcc×( R2/ (R1+R2))
Exemple
Pour les besoins de cet exemple, le montage précédent sera utilisé avec une tension Vcc égal à 9V, R1=1kΩ et R2=3 kΩ. Avec ces données il est possible de calculer facilement la valeur de la tension Va:
Va = Vcc×( R2/ (R1+R2))+R2)) = 9 ×(3000 / (1000+3000)) = 27000 / 4000 = 27/4 = 6.75V
La différence de potentiel Va sera égale à 6.75V en utilisant les valeurs précédentes.
Exercice corrigé sur le pont diviseur de tension
Soit le circuit ci-dessous :
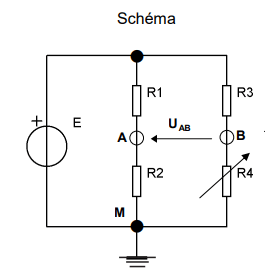
Lorsque le pont est équilibré, UAB = 0.
On se propose de calculer la résistance R4 (Capteur) permettant de remplir cette condition.
1) Donner l’expression littérale de VAM en fonction de E, R1 et R2
2) Donner l’expression littérale de VBM en fonction de E, R3 et R4.
3) Donner l’expression littérale de UAB en fonction de E, R1, R2, R3 et R4.
4) Former la condition d’équilibre : UAB = 0.
5) Donner l’expression littérale de R4 à l’équilibre en fonction de R1, R2 et R3.
6) Calculer la valeur de R4.
Les données :
- R1 = 10kΩ
- R2 = 1kΩ
- R3 = 2,2kΩ
- R4 = Capteur
- E = 12V
Solution
1) Donner l’expression littérale de VAM en fonction de E, R1 et R2
J’applique la loi du pont diviseur de tension : VAM = (E×R2)/ (R1+R2)
2) Donner l’expression littérale de VBM en fonction de E, R3 et R4.
J’applique la loi du pont diviseur de tension : VBM = (E×R4)/ (R3+R4)
3) Donner l’expression littérale de UAB en fonction de E, R1, R2, R3 et R4.
On a VAM = VA et VBM = VB
UAB = VA – VB = VAM – VBM = (E×R2)/ (R1+R2) – (E×R4)/ (R3+R4)
4) Former la condition d’équilibre : UAB = 0.
(E×R2)/ (R1+R2) – (E×R4)/ (R3+R4) = 0
5) Donner l’expression littérale de R4 à l’équilibre en fonction de R1, R2 et R3
On a (E×R2)/ (R1+R2) – (E×R4)/ (R3+R4) = 0
- R2/ (R1+R2) – R4/ (R3+R4) = 0
- R2/ (R1+R2) = R4/ (R3+R4)
- R2×(R3+R4) = R4×(R1+R2)
- R2×R3+ R2×R4 = R4×R1+ R4×R2
- R2×R3 = R4×R1
- R4 = R2×R3/R1
6) Calculer la valeur de R4.
On a R4 = R2×R3/R1
Application numérique :
- R4 = (103×2.2×103)/10×103
- R4 = 220 Ω