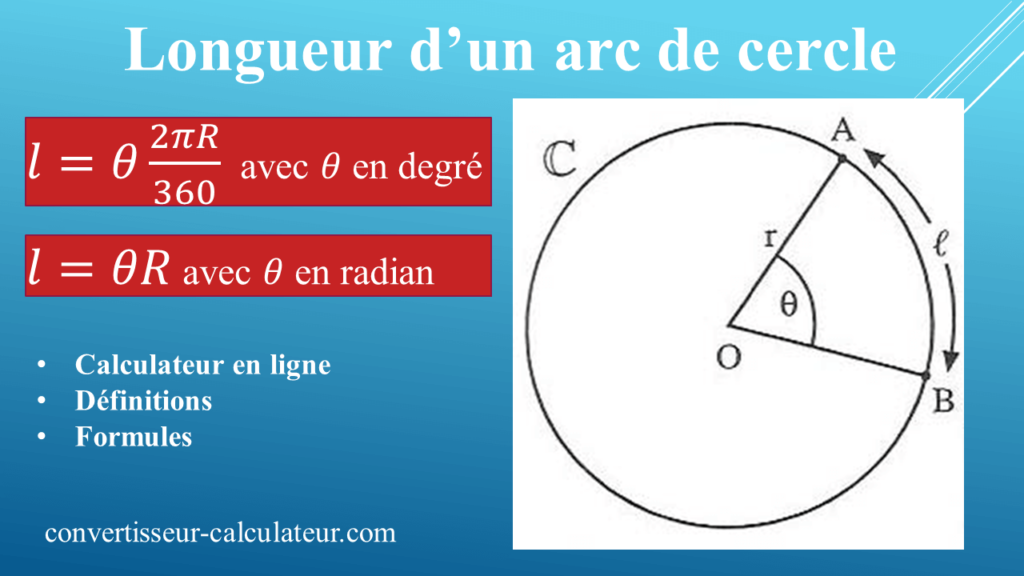
Longueur d’un arc de cercle : calculateur en ligne, Définitions et formules
Calculateur de longueur d’un arc de cercle
Définitions
- Un cercle est l’ensemble des points du plan situés à une distance constante (le rayon) d’un point donné (le centre).
- Un disque de centre O et de rayon r est l’ensemble des points du plan dont la distance à O est inférieure ou égale à r. (Il s’agit en fait de l’étendue, de la surface délimitée par la circonférence).
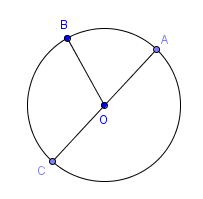
- Un rayon est un segment qui rejoint le centre du cercle, O, à un point sur le cercle, B. Le segment OB est un rayon.
- Un diamètre est un segment qui rejoint deux points du cercle et qui passe par le centre du cercle. Le segment AC est un diamètre parce qu’il est formé par deux points appartenant au cercle et qu’il passe par le centre du cercle, O.
- Un arc de cercle est un morceau de cercle délimité par deux points sur le cercle, A et B.
- Un angle est formé par deux demi-droites qui se rejoignent en un seul point, le sommet. Il existe plusieurs types d’angles :
- un angle aigu est un angle qui mesure moins que 90° ;
- un angle droit est un angle qui mesure 90°. Les côtés qui forment un angle droit sont perpendiculaires ;
- un angle obtus est un angle qui mesure plus que 90° mais moins que 180° ;
- un angle plat est un angle qui mesure exactement 180° ;
- un angle rentrant est un angle qui mesure plus que 180° mais moins que 360°.
Longueur d’un arc de cercle
Cas N°1 : l’angle au centre qui intercepte l’arc en degré
Soit le cercle de centre O et de rayon R.
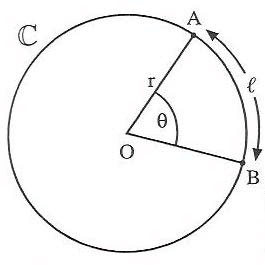
- La longueur du cercle est 2πR, d’un demi-cercle est πR et d’un quart de cercle est πR/2.
- La longueur d’un arc de cercle est proportionnelle à la mesure de l’angle au centre qui intercepte cet arc (donc la mesure de cet arc).
Si θ est la mesure en degré de l’angle au centre : AOB alors θ est la mesure en degré de l’arc AB
Soit l la longueur de l’arc AB (en unité de longueur m)
l = 2πθR/360
Exemple :
Exemples :
- θ =90° ===> l= πR/2.
- θ =60° ===> l= πR/3.
- θ =240° ===> l= 4πR/3.
Cas particulier : R = 1.
l = απ/180
Les valeurs usuelles :
| Mesure en degré des arcs | 0° | 30° | 60° | 90° | 120° | 150° | 180° |
| Longueurs des arcs | 0 | π/6 | π/3 | π/2 | 2π/3 | 5π/6 | π |
Cas N°2 : l’angle au centre qui intercepte l’arc en radians
Soit le cercle de centre O et de rayon R.
Si α est la mesure en radians d’un arc (ou de l’angle au centre qui intercepte cet arc) et l la longueur de cet arc.
l = Rα
Si de plus R = 1
l=α
Conséquence :
La mesure en radians d’un arc d’un cercle de rayon 1 est égale à la longueur de cet arc.
Voir aussi :
Autres sujets peuvent vous intéresser
Longueur d’un arc de cercle : calculateur en ligne, Définitions et formules
Longueur d’un arc de cercle : calculateur en ligne, Définitions et formules









