
Fraction irréductible : Simplification des fractions en ligne, définition, propriétés, règles et exercices corrigés
Simplification de fractions en ligne
Définition de fraction
Une fraction est notée sous la forme d’un quotient de 2 nombres entiers. Ces deux nombres sont séparés par un trait appelé barre de fraction.
Le nombre de la partie supérieure de la fraction est le numérateur. Le nombre de la partie inférieure de la fraction est le dénominateur ( le dominateur est toujours différent de 0) .
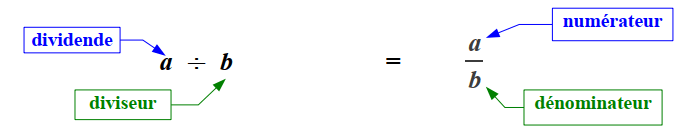
Pour lire une fraction, on lit d’abord le nombre du numérateur puis le nombre du dénominateur auquel on ajoute le suffixe « ièmes ».
Exemples :
- 4/7 : se lit quatre septièmes.
- 3/10 : se lit trois dixièmes.
Exceptions :
- ½ : se lit un demi.
- 1/3 se lit un tiers.
- 1/4 se lit un quart.
Propriétés des fractions
- Si le numérateur est inférieur au dénominateur, alors la fraction est inférieure à 1.
- Si le numérateur est supérieur au dénominateur, alors la fraction est supérieure à 1.
- Si le numérateur et le dénominateur sont égaux, alors la fraction est égale à 1.
- Le dénominateur doit toujours être différent de 0, car la division par 0 est indéfinie en mathématique.
Définition d’une fraction irréductible
Simplifier une fraction c’est diviser le numérateur et le dénominateur par un même nombre entier, le plus grand possible. Si on ne peut pas simplifier une fraction on dit qu’elle est IRREDUCTIBLE.
Pour simplifier, on se sert de la propriété suivante :
Pour tous réels a, b, k (avec b ≠ 0 et k ≠ 0),
\frac{k\times a}{k\times b}= \frac{a}{b}Ainsi, avant de simplifier un quotient, on factorise le numérateur et le dénominateur par un facteur commun.
Exemple : Simplifier 63/45.
\frac{63}{45}= \frac{9\times 7}{9\times 5}= \frac{7}{5}On dit qu’on a simplifié par 9.
Comment Simplifier une fraction
On décompose chaque nombre en produits d’entiers, en cherchant à faire apparaître un même diviseur au numérateur et au dénominateur.
Enfin on simplifie par ce diviseur commun.
Exemple :
\frac{15}{40}= \frac{5\times 3}{5\times 8}= \frac{3}{8}Parfois ont peut effectuer plusieurs étages :
\frac{144}{96}= \frac{2\times 72}{2\times 48}= \frac{72}{48}= \frac{9\times 8}{6\times 8}= \frac{9}{6}= \frac{3\times 3}{2\times 3}= \frac{3}{2}Remarque : au total on aura simplifié par 2 × 8 × 3 c’est à dire par 48.
Exercices corrigés sur la simplification des fractions
Exercice N°1
Rends la fraction 280/448 irréductible.
Réponse
On commence par décomposer 280 et 448 en produit de facteurs premiers.
280 = 2×2×2×7×5 et 448 = 2×2×2×2×2×2× 7
\frac{280}{448}= \frac{2\times2\times2\times 7 \times 5}{2\times2\times2\times2\times2\times2\times 7}= \frac{5}{2\times2\times2}= \frac{5}{8}qui est irréductible car 5 et 8 n’ont que 1 comme diviseur commun.
Exercice N°2
Les fractions sont-elles simplifiables ? Justifie.
- 4/6
- 3/19
- 15/30
- 1/82
- 42/39
Réponse
- Oui, car le numérateur et le dénominateur sont pairs et donc divisibles par 2,
- Non, car le numérateur et le dénominateur sont tous les deux premiers et 19 n’est pas un multiple de 3.
- Oui, car le numérateur et le dénominateur se terminent par 0 et 5 et sont donc divisibles par 5.
- Non, car le numérateur n’est divisible que par 1.
- Non car le numérateur et le dénominateur n’ont pas d’autre diviseur commun que 1..
Voir aussi :
Autres sujets peuvent vous intéresser
Fraction irréductible : Simplification des fractions en ligne, définition, propriétés, règles et exercices corrigés
Fraction irréductible : Simplification des fractions en ligne, définition, propriétés, règles et exercices corrigés
Fraction irréductible : Simplification des fractions en ligne, définition, propriétés, règles et exercices corrigés
Fraction irréductible : Simplification des fractions en ligne, définition, propriétés, règles et exercices corrigés









