
Energie potentielle de pesanteur : calculateur en ligne, définition, propriétés, formules et exercice corrigé
Calculateur de énergie potentielle de pesanteur
L’énergie potentielle correspond à l’énergie d’un système du fait de sa position dans l’espace.
L’énergie potentielle est en “réserve”, elle se manifeste quand elle se transforme en énergie cinétique.
On distingue différents types d’énergie potentielle :
- énergie potentielle de pesanteur
- énergie potentielle électrostatique
- énergie potentielle élastique
Définition de l’énergie potentielle de pesanteur
L’énergie potentielle de pesanteur d’un solide est l’énergie que possède un solide du fait de sa position par rapport à la terre. Elle résulte de l’interaction gravitationnelle entre le solide et la terre. Elle est notée Epp.
Cette énergie s’exprime en joules (J)
Propriétés
- L’énergie potentielle est une valeur algébrique;
- L’énergie potentielle de pesanteur augmente lorsque l’altitude augmente;
- Lorsque le système monte, il gagne en altitude donc il gagne en énergie potentielle de pesanteur : ∆Epp > 0;
- Si le système descend c’est l’inverse, il perd de l’énergie potentielle de pesanteur : ∆Epp < 0;
- Le niveau de référence des énergies potentielles de pesanteur peut être choisi de manière arbitraire;
- L’important est la variation d’énergie lorsqu’il y a une variation d’altitude;
- La variation de l’énergie potentielle ne dépend pas de l’état de référence.
Expression de l’énergie potentielle de pesanteur
On se place dans le champ de pesanteur terrestre supposé uniforme et d’intensité g.
Plus l’altitude augmente plus l’énergie potentielle doit être importante. L’énergie potentielle de pesanteur Epp a pour expression :
- Si l’axe Oz est orienté suivant la verticale ascendante :
Epp(z) = mgz + cte avec z ↑
- Si l’axe Oz est orienté vers le bas :
Epp(z) = −mgz + cte avec z ↓
Avant tout calcul de l’énergie potentielle de pesanteur, il faut déterminer la constante Cte . Pour cela :
- On oriente l’axe Oz vers le haut.
- On choisit comme état de référence Epp = 0,
Le plan horizontal passant par l’origine O où z = 0. Dans ce cas la constante Cte = 0. Donc l’énergie potentielle pour une position d’altitude z est :
Epp = mgz
- si z > 0 on a Epp > 0
- si z < 0 on a Epp < 0
Variation de l’énergie potentielle
La variation d’énergie potentielle de pesanteur entre un point A et un point B est donnée par la relation suivante :
∆Epp = Epp (B) − Epp (A) = mgzB − mgzA = mg (zB − zA)
∆Epp = mg (zB − zA)
Avec :
- Epp : L’énergie potentielle de_pesanteur(en J)
- m : La masse du système (en kg)
- g : l’intensité du champ de pesanteur (en m.s−2)
- z : l’altitude (en m)
Exercice corrigé
Enoncé
Sara, debout sur un pont, lance verticalement vers le haut une pierre de masse 𝑚 = 70 𝑘𝑔.
La pierre s’élève jusqu’à une hauteur de 10 𝑚 au-dessus du pont de lancement puis redescend et tombe dans l’eau.
La surface de l’eau est située 2 𝑚 plus bas que le point de lancement de la pierre.
1- calculer :
- L’énergie potentielle_de pesanteur de la pierre dans sa position la plus haute.
- L’énergie potentielle de pesanteur de la pierre dans sa position la plus basse.
- La variation de l’énergie potentielle de pesanteur de la pierre.
Si l’on choisit comme niveau de référence (origine de l’axe Oz dirigé vers le haut)
1-1- Le niveau du point de lancement de la pierre.
1-2- Le niveau de la surface de l’eau.
2- Quel conclusion pouvez-vous en tirer ?
Solution
1-1- Niveau de référence : le point de lancement de la pierre
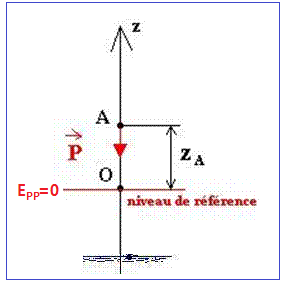
L’énergie potentielle de pesanteur de la pierre dans sa position la plus haute (point A).
𝐸𝑝𝑝(A) = 𝑚𝑔𝑧𝐴 = 0,07 × 10 × 10 = 7,0 𝐽
L’énergie potentielle de pesanteur de la pierre dans sa position la plus basse (point B).
𝐸𝑝𝑝(𝐵) = 𝑚𝑔𝑧𝐵 = 0,07 × 10 × (−2) = −1,4 𝐽
Variation d’énergie potentielle :
∆𝐸𝑃𝑃 = 𝐸𝑝𝑝(A) − 𝐸𝑝𝑝(𝐵) = 7,0 − (−1,4) = 8,4 𝐽
1-2- Niveau de référence : le point de surface de l’eau
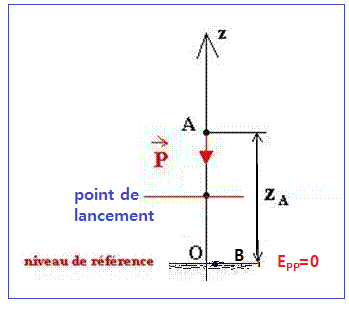
L’énergie potentielle de pesanteur de la pierre de point A.
𝐸𝑝𝑝(𝐴) = 𝑚𝑔𝑧𝐴 = 0,07 × 10 × 12 = 8 ,4 𝐽
L’énergie potentielle de pesanteur de la pierre de point B (état de référence).
𝐸𝑝𝑝(𝐵) = 𝑚𝑔𝑧𝐵 = 0
Variation d’énergie potentielle :
∆𝐸𝑃𝑃 = 𝐸𝑝𝑝(𝐴) − 𝐸𝑝𝑝(𝐵) = 8,4 − 0 = 8,4 𝐽
2- Conclusion :
La variation de l’énergie potentielle ne dépend pas de l’état de référence contrairement à l’énergie potentielle.











