
Division des fractions : calcul en ligne, définition, propriétés, règles et exercices corrigés
Division des fractions en ligne
Définition de fraction
Une fraction est notée sous la forme d’un quotient de 2 nombres entiers. Ces deux nombres sont séparés par un trait appelé barre de fraction.
Le nombre de la partie supérieure de la fraction est le numérateur. Le nombre de la partie inférieure de la fraction est le dénominateur ( le dominateur est toujours différent de 0) .
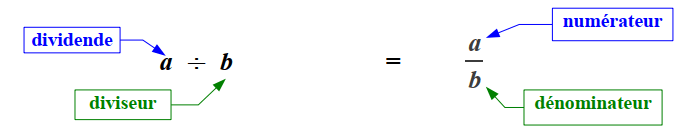
Pour lire une fraction, on lit d’abord le nombre du numérateur puis le nombre du dénominateur auquel on ajoute le suffixe « ièmes ».
Exemples :
- 4/7 : se lit quatre septièmes.
- 3/10 : se lit trois dixièmes.
Exceptions :
- ½ : se lit un demi.
- 1/3 se lit un tiers.
- 1/4 se lit un quart.
Propriétés des fractions
- Si le numérateur est inférieur au dénominateur, alors la fraction est inférieure à 1.
- Si le numérateur est supérieur au dénominateur, alors la fraction est supérieure à 1.
- Si le numérateur et le dénominateur sont égaux, alors la fraction est égale à 1.
- Le dénominateur doit toujours être différent de 0, car la division par 0 est indéfinie en mathématique.
- Si a est entier non nul, l’inverse de a est 1/a. (Il n’existe aucun nombre qui, multiplié par 0, donne 1 donc 0 n’a pas d’inverse)
- Lorsque a et b sont des entiers non nuls, l’inverse de a/ b est b/a.
Comment diviser les fractions ?
La règle permet donc de transformer une division de fraction en une multiplication.
Diviser une fraction par un nombre
Pour diviser une fraction par un nombre, on divise si c’est possible, le numérateur par le nombre et on conserve le dénominateur.
Exemple :
Papa partage équitablement les 2/3 du gâteau ci-dessous entre ses deux enfants. Quelle est la part de chaque enfant ?
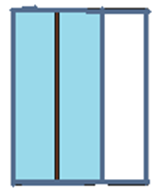
Chaque enfant aura 1/3 du gâteau. Donc :
\frac{2}{3}\div 2 = \frac{2\div 2}{3}= \frac{1}{3}
On a divisé le numérateur par 2.
Remarque
Remarquant que :
2=\frac{2}{1} \quad, on \quad a \quad \frac{2}{3}\div 2 = \frac{\frac{2}{3}}{2} =\frac{\frac{2}{3}}{\frac{2}{1}}= \frac{2}{3}\times \frac{1}{2}= \frac{1}{3}Pour diviser une fraction par un nombre, on multiplie la fraction par l’inverse du nombre
Diviser un nombre par une fraction
Pour diviser un nombre par une fraction, on multiplie ce nombre par l’inverse de la fraction.
Exemple :
Abdalah met 4 kg de sucre dans des sachets de 2/3kg. Trouve le nombre de sachets.
Réponse
\frac{4}{\frac{2}{3}}= 4\times \frac{3}{2}= \frac{4\times 3}{2}= 6Le nombre de sachets est égale à 6
Diviser une fraction par une fraction
Pour diviser une fraction par une fraction, il faut multiplier la fraction dividende par l’inverse de la fraction diviseur.
Exemple :
Maman met 9/4 kg de piment dans des sachets de 3/4kg. Trouve le nombre de sachets.
Réponse
\frac{\frac{9}{4}}{\frac{3}{4}}= \frac{9}{4}\times \frac{4}{3}= 3Le nombre de sachets est égale à 3
Exercice corrigé sur la division des fractions
Calculer et simplifier 𝟏𝟐/𝟐𝟓 ÷ 𝟏𝟔/𝟑𝟓
Méthode 1 :
\frac{12}{25}\div \frac{16}{35} = \frac{12}{25}\times \frac{35}{16} =\frac{12\times 35}{25\times16}=\frac{4\times 3\times 7\times 5}{5\times5 \times 4 \times4}= \frac{21}{20}Méthode 2 : Nous pouvons aussi décomposer en produit de facteurs premiers
\frac{12}{25}\div \frac{16}{35} = \frac{12}{25}\times \frac{35}{16} =\frac{12\times 35}{25\times16}=\frac{2\times 2\times 3\times 7\times 5}{5\times5 \times 2\times 2 \times2\times 2}= \frac{21}{20}Voir aussi :
Autres sujets peuvent vous intéresser
Division des fractions : calcul en ligne, définition, propriétés, règles et exercices corrigés
Division des fractions : calcul en ligne, définition, propriétés, règles et exercices corrigés
Division des fractions : calcul en ligne, définition, propriétés, règles et exercices corrigés
Division des fractions : calcul en ligne, définition, propriétés, règles et exercices corrigés
Division des fractions : calcul en ligne, définition, propriétés, règles et exercices corrigés
Division des fractions : calcul en ligne, définition, propriétés, règles et exercices corrigés









