Circuit RC série : Calculateur en ligne, définitions, formules et exercice corrigé
Calculateur en ligne
Définition de l’impédance
L’impédance est une grandeur qui généralise la notion de résistance, de réactance capacitive et de réactance inductive dans le cas des circuits comportant plusieurs éléments de nature différente. Elle caractérise la manière dont le circuit freine le passage du courant en donnant le rapport qui existe entre la tension de la source de f.é.m. et le courant résultant.
Toutefois, comme dans le cas d’un circuit avec seulement un condensateur ou seulement un inducteur, il y a un déphasage entre tension et courant qui fait qu’ils ne passent pas en même temps par leur maximum et qu’on ne peut prendre le rapport des valeurs instantanées, v/i, pour caractériser le circuit ; en effet, ce rapport varie dans le temps. Par contre on peut le faire soit avec le rapport des amplitudes ou des valeurs efficaces, comme dans le cas des réactances, soit avec le rapport des phaseurs. Dans ce dernier cas, on définit une impédance complexe.
L’impédance d’une résistance
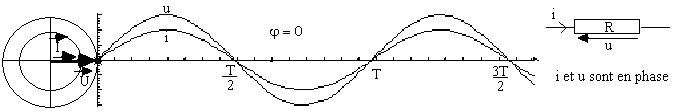
L’impédance d’une résistance est indépendante de la fréquence du courant alternatif qui le traverse, elle est égale à la résistance R du conducteur ohmique.
ZR = |ZR|= R
L’impédance d’un condensateur
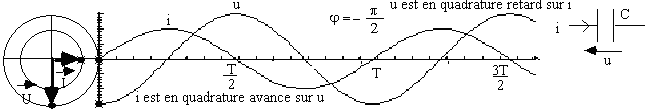
Un condensateur est caractérisé par sa capacité, notée C. L’unité légale de mesure de la capacité est le farad, dont le symbole est F. Les unités couramment utilisées sont le microfarad (1µF = 10-6 F) et le picofarad (1pF = 10-9 F).
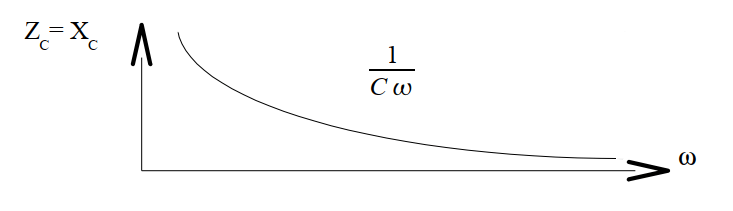
L’impédance d’un condensateur, que l’on appelle aussi sa réactance de capacité, notée XC est inversement proportionnelle à sa capacité et à la pulsation ω du courant.
Un condensateur oppose d’autant moins de « résistance » au passage du courant alternatif que sa capacité est grande et la fréquence élevée.
ZC = XC = 1/ωC et ω = 2πf
Avec :
- ω : Pulsation en rad/s
- f : Fréquence en hertz (Hz))
- C : Capacité du condensateur en farad
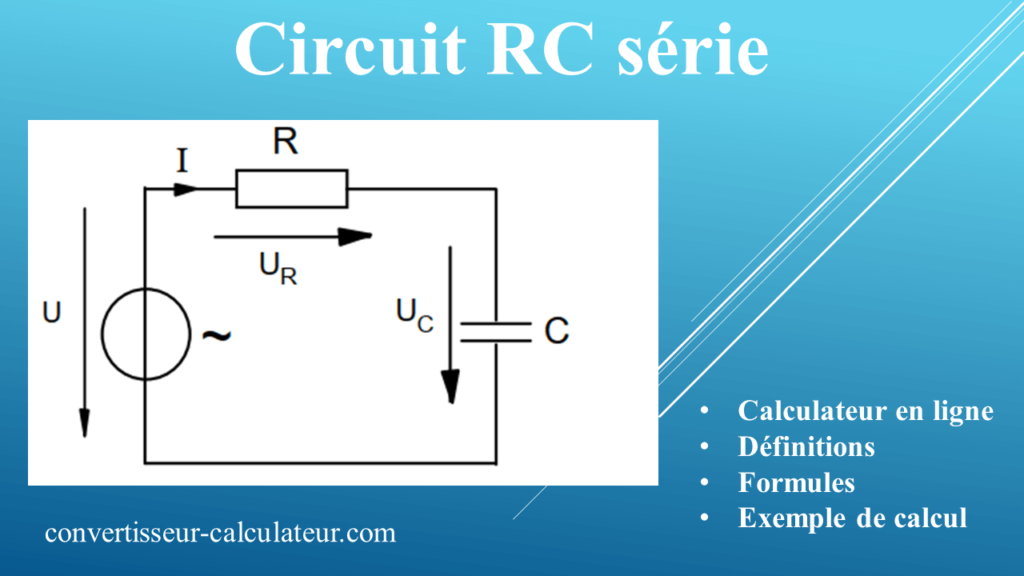
Calcul d’impédance d’un circuit RC série
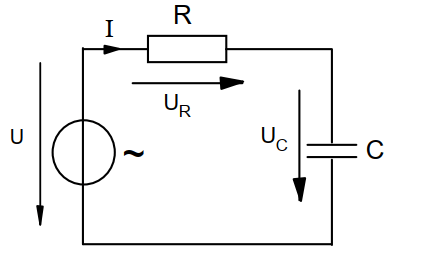
Ce circuit est plutôt rencontré dans les appareils électroniques pour filtrer certaines fréquences. En électricité, les condensateurs sont utilisés pour corriger les déphasages provoqués par les récepteurs inductifs (moteurs, ballast TL, etc.).
Suivant le montage, il est possible de trouver des condensateurs en série avec une résistance. Pour réaliser des adaptations en tension en introduisant un condensateur en série avec une charge résistive (réducteur de tension). Ce montage peut également être réalisé au moyen d’une bobine montée en série avec la charge résistive. Les circuits RC réducteurs de tension sont plus souvent utilisés car les condensateurs sont en général de plus petite taille et d’un coût plus bas.
Diagramme vectoriel d’un circuit RC série
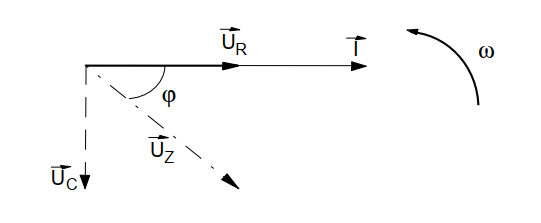
La résistance ne provoque pas de déphasage et sa tension UR est en phase avec le courant.
La tension UC est en retard de 90 ° par rapport au courant. La tension U aux bornes du circuit est la résultante de l’addition vectorielle des tensions UR et UC.
Pour trouver cette résultante, nous pouvons également appliquer les relations de Pythagore.
Uz = √(UR2+ UC2)
Impédance total du circuit RC série
La notion d’impédance est également utilisée avec ce circuit, donc :
Z = √(R2+ XC2) avec XC = 1/ωC = 1/2.π.f.C
Déphasage du circuit RC série
L’angle de déphasage est déterminé de la manière suivante :
cosϕ = R/Z= UR/UZ ⇒ ϕ = cos-1(R/Z) = cos-1(UR/UZ )
Exercice corrigé – circuit RC série
Un circuit RC série composé d’une résistance de 120 Ω et d’un condensateur de 15 µF. Il est raccordé sur une source de tension de 100 V dont la fréquence est de 60 Hz.
Calculer l’impédance, toutes les tensions, le courant et l’angle de déphasage.
Solution
Données : R = 120 Ω ; C = 15 µF ; U = 100 V ; f= 60 Hz.
Inconnues : Z ; UR ; UC ; I ; ϕ
a- Calcul de la réactance capacitive :
XC = 1/ωC = 1/2.π.f.C = 1/(2×π×60×15×10-6)
XC = 176.84 Ω
b- Calcul de l’impédance :
Z = √(R2+ XC2) = √(1202+ 176.84 2)
Z = 213.71 Ω
c- Calcul du courant :
I = UZ/Z = 100/213.71
I = 468 mA
d- Calcul des tensions :
- UR = R.I = 120×468×10−3 = 56.16 V
- UC = XC.I = 176.84×468×10−3 = 82.76 V
Contrôle du calcul des tensions :
U = √(UR2+ UC2) = √(56.162+ 82.762) = 100 V
e- Calcul du déphasage :
- ϕ = cos-1(R/Z) = cos-1(120/213.71) = 55.84°
- ϕ = cos-1(UR/UZ) = cos-1(56.16/100) = 55.84°
Voir aussi :
Autres sujets peuvent vous intéresser
Circuit RC série : Calculateur en ligne, définition, formules et exemple de calcul