Force électrostatique – Loi de Coulomb : calcul en ligne, formules et exemple de calcul
Calcul de la force électrostatique – Loi de Coulomb
Loi de Coulomb – force électrostatique
La loi de Coulomb exprime les forces électrostatiques s’exerçant entre deux charges électriques ponctuelles, immobiles et placées dans le vide.
Les forces d’interaction coulombienne sont :
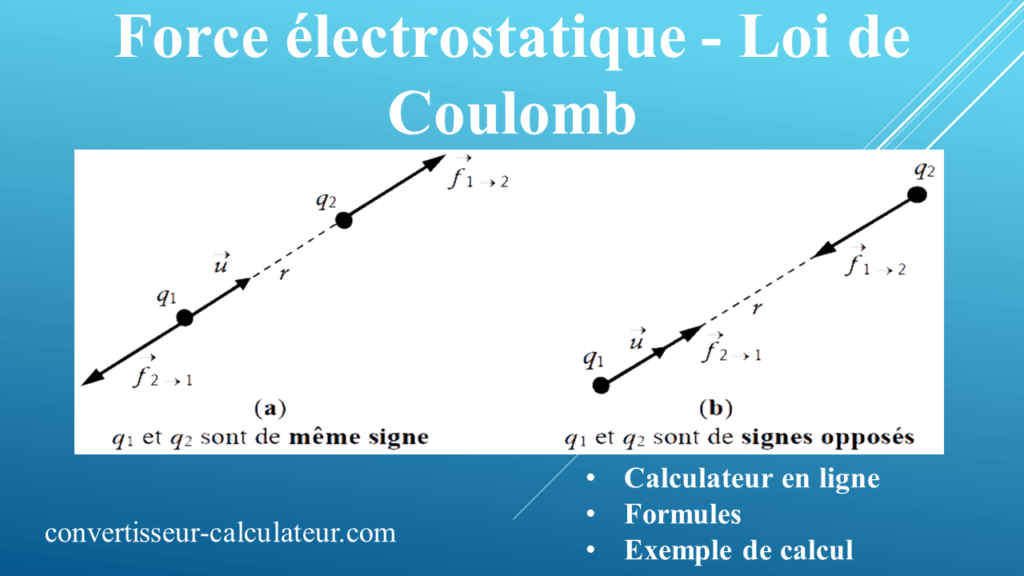
- soit répulsives si les charges sont de même signe ;
- soit attractives lorsque les charges sont de signes opposés.
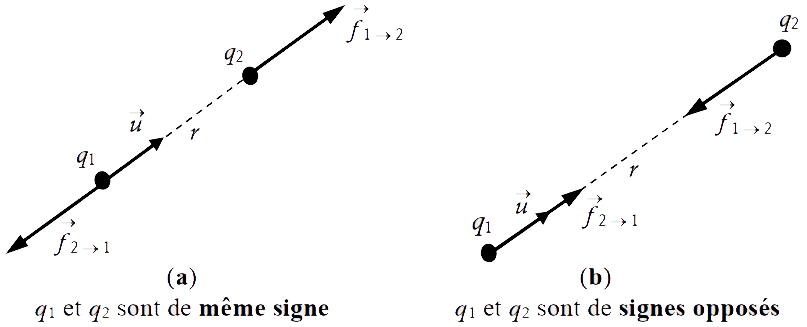
En vertu de la loi de Coulomb, la force fij exercée par la charge qi sur la charge qj est égale et opposée à la force fji exercée par la charge qj sur la charge qi, soit :
Cas de forces répulsives.
\overrightarrow{f_{1\mapsto 2}}= \frac{1}{4\pi \varepsilon_{0} }\frac{q_{1}q_{2}}{r^{2}}\overrightarrow{u}\overrightarrow{f_{2\mapsto 1}}= -\frac{1}{4\pi \varepsilon_{0} }\frac{q_{1}q_{2}}{r^{2}}\overrightarrow{u}\Rightarrow \overrightarrow{f_{1\mapsto 2}}= -\overrightarrow{f_{2\mapsto 1}}Cas de forces attractives
\overrightarrow{f_{1\mapsto 2}}= -\frac{1}{4\pi \varepsilon_{0} }\frac{q_{1}q_{2}}{r^{2}}\overrightarrow{u}\overrightarrow{f_{2\mapsto 1}}= \frac{1}{4\pi \varepsilon_{0} }\frac{q_{1}q_{2}}{r^{2}}\overrightarrow{u}\Rightarrow \overrightarrow{f_{1\mapsto 2}}= -\overrightarrow{f_{2\mapsto 1}}On pose souvent : K = 1/(4πε0)=9 ×109 N.m2/C2.
- ε0 : permittivité diélectrique du vide, approximativement : ε0 = 8,84 ×10-12 F.m-1;
- r : distance entre les deux charges q1 et q2 ;
Remarque
L’unité de la permittivité diélectrique du vide vient de la relation de définition de la capacité C d’un condensateur plan dont les armatures distantes de d, ont une surface S et sont séparées par le vide :
C = ε0S/d ==> ε0 = C.d/S. C en fard (F), d en mètre (m), S en mètre-carré (m2) ; d’où ε0 s’exprime en Farad par mètre (F.m-1)
Norme de la force électrostatique
Les deux forces fi j ont même norme :
f_{1\mapsto 2}= \frac{1}{4\pi \varepsilon_{0} }\frac{\left| q_{1}q_{2}\right|}{r^{2}} = k\frac{\left| q_{1}q_{2}\right|}{r^{2}}Avec :
- f : La force électrostatique en newton (N);
- q1, q2 : Charges électriques en coulomb (C);
- r : Distance entre les deux charges en mètre (m);
- k : Constante de coulomb en N.m2/C2.
Force électrostatique résultante entre plusieurs charges -Principe de superposition
On considère la répartition de charges du schéma suivant. Quelle est la force totale subite par la particule de charge q3 ?
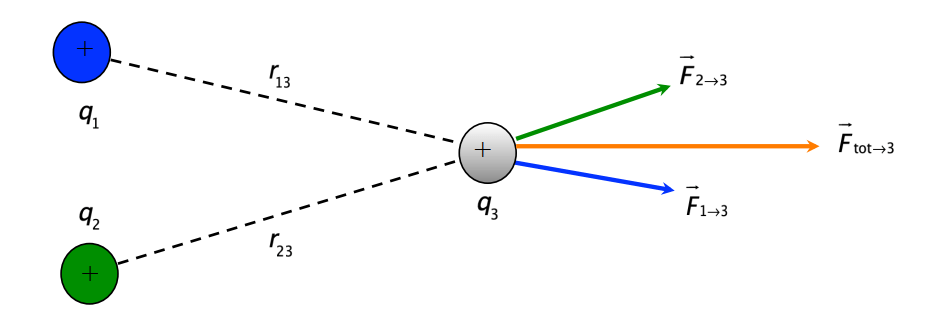
La loi de Coulomb décrit uniquement l’interaction entre deux charges. Mais l’expérience montre que lorsque deux charges exercent simultanément une force sur une troisième charge, la force totale sur cette dernière est la somme vectorielle des forces que les deux charges exercent individuellement. On a donc simplement Ftot-3=F1-3=F2-3. Ce résultat se généralise à une distribution quelconque de plusieurs charges. Il s’agit du principe de superposition qui joue un rôle très important dans l’étude de l’électromagnétisme.
Donc la résultante des forces électrostatiques exercées par un ensemble de N charges ponctuelles qi fixes, sur une charge ponctuelle q fixe placée à une distance ri de chaque charge qi, est donnée par la relation suivante :
\overrightarrow{F}= k.\frac{qq_{1}}{r_{1}^{2}}\overrightarrow{u_{1}} = k.\frac{qq_{2}}{r_{2}^{2}}\overrightarrow{u_{2}} = k.\frac{qq_{3}}{r_{3}^{2}}\overrightarrow{u_{3}} + ...= k\sum_{i= 1}^{N}\frac{qq_{i}}{r_{i}^{2}}\overrightarrow{u_{i}}ui: vecteur unitaire dirigé de la charge qi vers la charge q.
Exemple
Calculer la force électrostatique sur la charge q1 = 20µC, par une charge q2 = −300µC et la distance être les deux charges est égale à r = 3m.
Selon la description du problème, on cherche F2-1.
alors,
f_{2\mapsto 1}= \frac{1}{4\pi \varepsilon_{0} }\frac{\left| q_{1}q_{2}\right|}{r^{2}} = k\frac{\left| q_{1}q_{2}\right|}{r^{2}}Application numérique
f_{2\mapsto 1} = 9\times10^{9}\times\frac{\left| 20\times10^{-6} \times -300\times10^{-6} \right|}{3^{2}}f_{2\mapsto 1} = 6NLa force électrostatique a une amplitude de 6N. Remarquer que la force de q1 sur q2 aura la même amplitude, mais sera de sens contraire.
Voir aussi :
Autres sujets peuvent vous intéresser
Force électrostatique – Loi de Coulomb : calcul en ligne, formules et exemple de calcul
Force électrostatique – Loi de Coulomb : calcul en ligne, formules et exemple de calcul
Force électrostatique – Loi de Coulomb : calcul en ligne, formules et exemple de calcul