L’éclairement lumineux : Calcul en ligne, définition, formule, exercice corrigé, mesure et ordres de grandeur
Calculateur de l’éclairement lumineux
Définition
L’éclairement décrit la densité du flux lumineux en un point d’une surface.
Soit une surface S placée à une distance d donnée de la source reçoit un éclairement E. C’est le flux reçu Φreçu par unité de surface éclairée. Il s’exprime en lux (lx).
1 lux correspond à un éclairement de 1 lm/m2, c’est-à-dire l’éclairement reçu par la calotte sphérique (surface S) que découpe, sur une sphère de 1m de rayon (R), “l’enveloppe” d’ un flux de 1 lm uniformément réparti dans un angle solide de 1 sr.
Formule de calcul de l’éclairement E
Formule générale d’éclairement est :
E = Φreçu/Surface
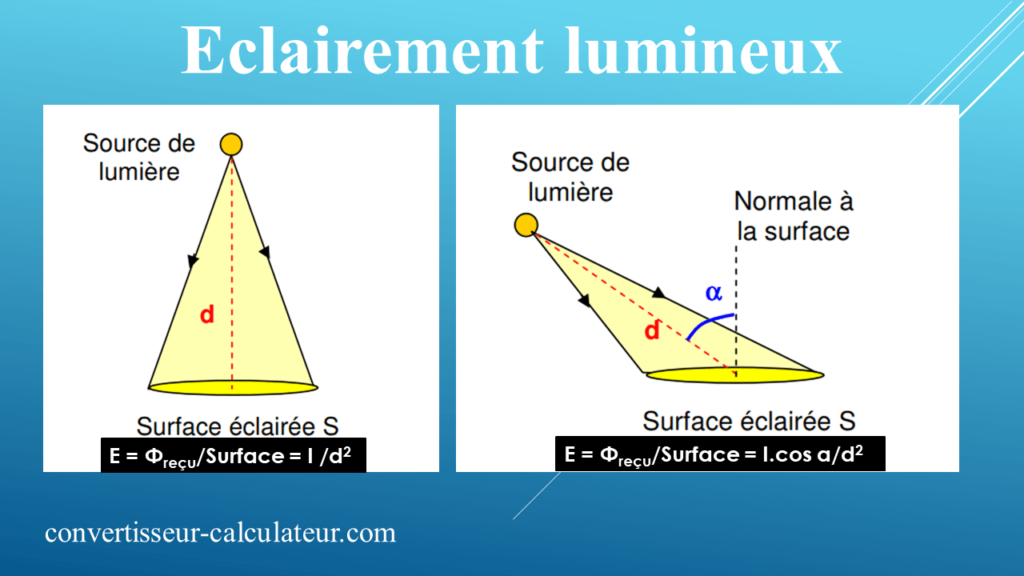
Si la direction principale d’émission est parallèle à la normale à la surface :
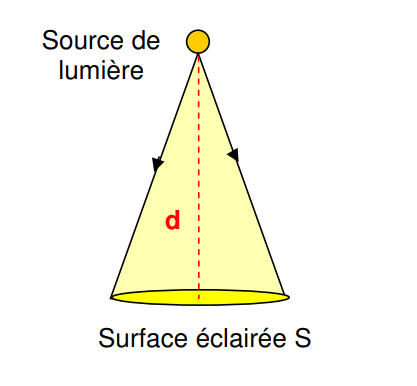
E = Φreçu/Surface = I /d2
Si la direction principale d’émission n’est pas parallèle à la normale à la surface :
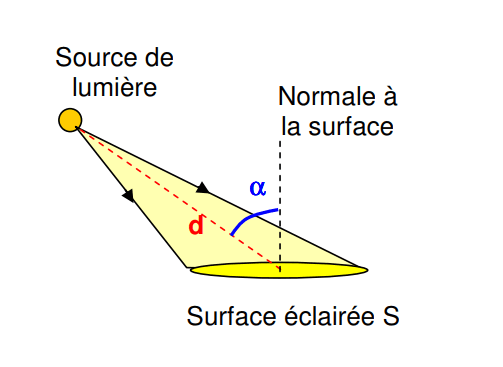
E = Φreçu/Surface = I.cos α/d2
Avec :
- E : L’éclairement lumineux en lux (lx) ;
- I : L’intensité lumineuse en candela (cd) ;
- Φreçu : Le flux reçu en lumen (lm) ;
- S : La surface éclairée en m2 ;
- d : La distance entre la source et la surface en m ;
- α : L’angle entre la direction principale d’émission et la normale à la surface éclairée.
Cas particulier :
E = I.cosα3 / h2
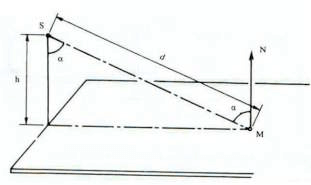
On retrouve ici un triangle rectangle où :
- d représente l’hypoténuse
- h représente le côté adjacent
- cos α = h /d
Donc E = I cos α / d2 devient E = I cos α x cos α2 / h2 = I cos α3 / h2
Remarques sur l’éclairement
- L’éclairement se donne toujours par rapport à une surface, horizontale (table, atelier…), verticale (mur, tableau…) ou oblique. L’éclairement n’est pas limité à des surfaces planes mais s’applique également à l’éclairement sphérique, cylindrique…
- l’éclairement est indépendant de la nature de la surface, mais dépend : de l’intensité lumineuse arrivant dans une direction donnée ; de la distance à la source et de l’inclinaison de la surface éclairée.
- Les formules sont valables pour des sources ponctuelles (valable si la distance, par rapport aux dimensions de la source, est suffisamment grande).
- Il est très difficile de comparer deux éclairements entre eux
Ordres de grandeur
| Sources | Eclairement E en lux |
| Pleine lune, ciel sans nuage | 0.2 |
| Bougie de ménage à 1m | 1 |
| Route / Rue éclairée | 20 à 30 |
| Aube, crépuscule | 50 |
| Bureau normalement éclairé | 400 |
| Eclairement horizontal extérieur à temps couvert | 5000 |
| Eclairement horizontal extérieur à beau temps | 10 à 20000 |
| Eclairement horizontal extérieur maximum mesurable | 100000 |
Mesure de l’éclairement
L’éclairement se mesure avec un luxmètre. C’est un appareil muni d’une cellule photoélectrique qui transforme l’énergie de rayonnement en énergie électrique. Pour que la lecture ne soit pas qu’une lecture de courant électrique (en Ampères) il est nécessaire d’interposer dans le circuit un filtre qui restitue une courbe de réponse identique à celle de l’œil humain standard. La surface de la cellule doit en outre être revêtue d’un filtre diffusant qui joue le rôle de correcteur d’incidence.
Exercice corrigé
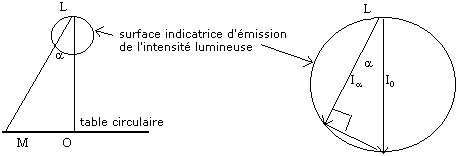
1. Une table circulaire de centre O et de diamètre D=2 m est éclairée par une source placée en L à une distance OL=h=2 m. Le constructeur précise que la surface indicatrice d’émission est une sphère passant par la source, dont le centre est placé sur la verticale. Cela signifie que la source ne rayonne pas dans toutes les directions de l’espace avec la même intensité lumineuse. L’angle solide dans lequel rayonne cette source est alors Ω = π st. Cette source, de puissance électrique P=100W a une efficacité lumineuse k=40 lmW-1.
a- Calculer le flux lumineux émis par cette source :
- φ = P x k = 100 x 40 = 4000 lm
b- Donner l’expression littérale de l’intensité lumineuse Iα et de I0. Calculer I0 et Iα :
- φ = π I0 —> I0 = φ / π = 4000 / π = 1273 Cd
- tg α = OM / OL = 1 / 2 = 0,5 —> α = 26,6°
- Iα = I0.cos α = 1273 x 0,894 = 1139 Cd
c- Calculer l’éclairement au centre de la table puis au bord de la table :
- E0= I0 / h² = 1273 / 2² = 318 lx
- E= E0.cos3 α = 318 x 0,715= 227 lx
2. Dans le cas d’une source émettant le même flux lumineux avec une intensité constante dans toutes les directions
a- Préciser la surface indicatrice d’émission :
- Sphère
b- Calculer l’intensité lumineuse I’0 :
- φ = 4 π I’0 —> I’0 = φ / 4 π = 4000 / 4 π = 318 Cd
c- Calculer l’éclairement lumineux E’0 au centre O de la table
- E’0 = I’0 / OL² = 318 / 2² = 79 lx