
Prisme droit : calcul de volume, définition, représentation, formule et exemple de calcul
Calculateur du volume d’un prisme droit
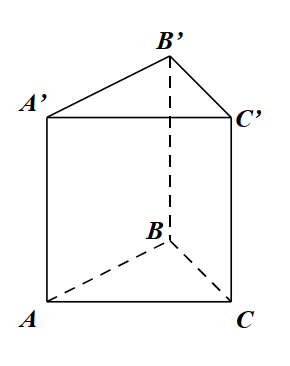
Définition du prisme droit
Un prisme_droit est un solide dont :
- Les deux bases sont des polygones (triangles, quadrilatères…). Elles sont parallèles.
- Les autres faces sont des rectangles et sont appelées les faces latérales : ABB’A’ , ACC’A’ et BCC’B’.
- L’arête [AA’] est perpendiculaire à la face ABC
- La distance entre les deux bases, c’est à dire AA’ ou BB’ ou CC’ est appelée hauteur du prisme_droit.
Remarque : Le pavé droit (parallélépipède rectangle) est un prisme droit particulier : ses deux bases sont aussi des rectangles.
Représentation en perspective cavalière
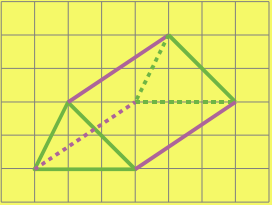
Les bases de ce prisme droit sont des triangles parallèles et superposables. On les représente en vraie grandeur.
Les arêtes latérales de ce prisme sont parallèles et de même longueur. On les représente par des segments parallèles de même longueur.
On trace en pointillés les arêtes cachées.
Type des prismes selon la géométrie des bases
- Prisme triangulaire : Ses bases sont des triangles.
- Prisme carré : Ses bases sont carrées.
- Prisme polygonale: Les bases du prisme sont des polygones.
Comment calculer le volume d’un prisme droit ?
Pour calculer le volume d’un prisme_droit ou d’un cylindre de révolution, on multiplie l’aire d’une base par la hauteur :
V = Abase × h.
Exemple
Détermine le volume du prisme_droit suivant :
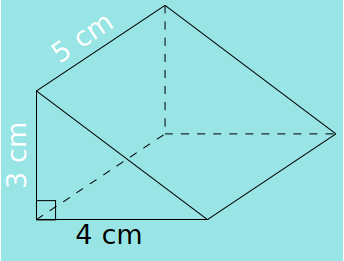
On calcule l’aire d’une base qui est un triangle rectangle :
Abase = (4 × 3) / 2 = 6 cm².
On multiplie l’aire d’une base par la hauteur :
V = Abase × h = 6 cm² × 5 cm = 30 cm3.
Le volume de ce prisme vaut 30 cm3









