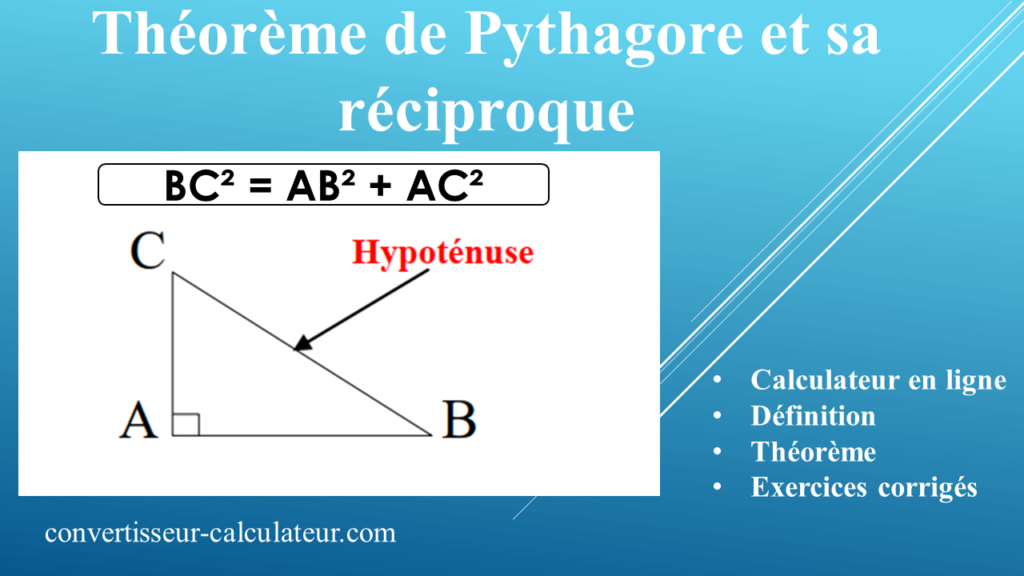
Théorème de Pythagore et sa réciproque: calcul en ligne, définition, théorème et exercices corrigés
Calculateur du théorème de Pythagore
Hypoténuse d’un triangle rectangle
Dans un triangle rectangle, le côté opposé à l’angle droit est le plus grand des trois côtés. On l’appelle l’hypoténuse du triangle.
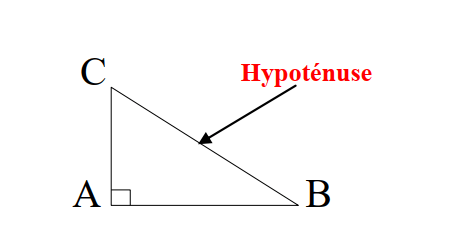
Enoncé du théorème de Pythagore
Si un triangle est rectangle alors le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.
Si ABC est un triangle rectangle en A alors :
BC² = AB² + AC²
Remarque : Le théorème de Pythagore ne s’applique qu’aux triangles rectangles.
Dans un triangle rectangle, le théorème de Pythagore permet de calculer la longueur d’un côté connaissant les longueurs des deux autres côtés.
Exemple : ABC est un triangle rectangle en A tel que AC = 8 cm et BC = 20 cm.
Calculer un arrondi à 0,1 cm près la longueur AB.
On sait que le triangle ABC est rectangle en A.
Si un triangle est rectangle alors le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés (théorème de Pythagore)
Donc :
- BC² = AB² + AC²
- 20² = AB² + 8²
- 400 = AB² + 64
- AB² = 400 – 64
- AB² = 336
On cherche un nombre positif qui a pour carré 336.
Donc AB ≈18,3 cm.
Démontrer qu’un triangle est rectangle ou non
Démontrer qu’un triangle est rectangle – Réciproque du théorème de Pythagore
Si, dans un triangle, le carré de la longueur du plus grand côté est égal à la somme des carrés des longueurs des deux autres côtés alors ce triangle est rectangle et l’angle droit est l’angle opposé au plus grand côté.
Si, dans un triangle ABC, BC² = AB² + AC² alors le triangle est rectangle en A.
La réciproque du théorème de Pythagore permet de démontrer qu’un triangle est rectangle.
Exemple :
Démontrer que le triangle ABC, tel que AB = 3,3 BC = 6,5 et AC = 5,6 est un triangle rectangle.
- BC ² = 6,5² = 42,25
- AB ² + AC ² = 3,3² + 5,6² = 10,89 + 31,36 = 42,25
- Donc BC² = AB² + AC².
On a l’égalité de Pythagore, donc le triangle est rectangle en A.
Démontrer qu’un triangle n’est pas rectangle
Si le carré de la longueur du plus grand côté d’un triangle n’est pas égal à la somme des carrés des longueurs des deux autres côtés alors ce triangle n’est pas rectangle.
Exemple :
Le triangle ABC de côtés AB = 2, AC = 3 et BC = 4 est-il rectangle ?
BC est le plus grand côté et BC2 = 16
AB² + AC² = 13
Donc BC² ≠ AB² + AC
Donc le triangle ABC n’est pas rectangle.
Exercices corrigés sur le théorème de Pythagore
Exercice N°1 :
Dans le triangle ABC rectangle en A on a : AB = 7,6cm et AC = 5,7cm.
Calculer la longueur du coté BC.
Le triangle ABC est rectangle en A donc l’hypoténuse est le côté BC.
Le théorème de Pythagore donne : BC2 = AB2 +AC2
BC2 = 7,62 +5,72
BC2 = 57,76+32,49 = 90,25
Donc BC = √90,25 = 9,5cm
Exercice N°2 :
Dans le triangle RAS on a : AR = 13,5m, RS = 8,1m et AS = 10,8m.
Démontrer que le triangle RAS est rectangle. On précisera en quel point.
AR est le plus grand coté du triangle RAS ; AR2 = 13,52 = 182,25.
RS2 +AS2 = 8,12 +10,82 = 65,61+116,64 = 182,25.
On constate qu’on a l’égalité : AR2 = RS2 +AS2.
Donc d’après la réciproque du théorème de Pythagore, le triangle RAS est rectangle en S.
Exercice N°3 :
Dans le triangle RST on a : TR = 6,6cm, RS = 5,3cm et T S = 4cm.
Démontrer que le triangle RST n’est pas rectangle.
TR est le plus grand coté du triangle RST ; TR2 = 6,62 = 43,56.
RS2 +TS2 = 5,32 +42 = 28,09+16 = 44,09.
On constate qu’on a l’inégalité : TR2 = RS2 +TS2.
Donc le triangle RST n’est pas rectangle
Exercice N°4 :
Dans le triangle IJK rectangle en I on a : IJ = 45mm et JK = 75mm.
Calculer la longueur du côté IK.
Le triangle IJK est rectangle en I donc l’hypoténuse est le côté JK.
Le théorème de Pythagore donne : JK2 = IJ2 +IK2
752 = 452 +IK2
5625 = 2025+IK2
Soit IK2 = 5625−2025 = 3600
Donc IK = √3600 = 60mm









