
Polygone régulier : Calcul en ligne, définition, construction de quelques polygones réguliers et formules
Calculateur d’aire d’un polygone régulier
Définition
On appelle polygone une figure fermée constituée de segments. Si n est un entier supérieur ou égal à 3, un polygone à n côtés contient n segments et n sommets, qui sont les extrémités des segments, chaque sommet étant commun à exactement deux côtés parmi les n.
On dit qu’il est croisé si au moins deux côtés se coupent ailleurs qu’aux sommets. Sinon, il est dit non croisé.
On appelle diagonale d’un polygone un segment joignant deux sommets non adjacents. On montre que, si n est le nombre de côtés, le nombre de diagonales est : n.( n-3)/2
Un polygone non croisé est dit convexe si toutes ses diagonales sont à l’intérieur de la surface délimitée par le polygone. Dans le cas contraire, donc si au moins une diagonale est à l’extérieur du polygone (non croisé), il est dit non convexe, ou encore concave.
On appelle polygone régulier un polygone dont les côtés sont de même longueur mais aussi tel que les sommets sont sur un même cercle. Le cercle est donc circonscrit au polygone.
Les polygones réguliers à 3 et 4 côtés s’appellent respectivement des triangles équilatéraux et des carrés.
Les rayons d’un polygone régulier sont les segments joignant les sommets au centre du cercle circonscrit au polygone.
Types de polygone
On nomme un polygone en fonction du nombre de ses côtés :
- Un polygone à 3 côtés est un triangle équilatéral,
- Un polygone à 4 côtés est un carré,
- Un polygone à 5 côtés est un pentagone,
- Un polygone à 6 côtés est un hexagone,
- Un polygone à 7 côtés est un heptagone,
- Un polygone à 8 côtés est un octogone,
- Un polygone à 9 côtés est un ennéagone,
- Un polygone à 10 côtés est un décagone,
- Un polygone à 11 côtés est un hendécagone,
- Un polygone à 12 côtés est un dodécagone,
- Un polygone à 13 côtés est un tridécagone,
- Un polygone à 14 côtés est un tétradécagone,
- Un polygone à 15 côtés est un pentadécagone,
- Un polygone à 16 côtés est un hexadécagone,
- Un polygone à 17 côtés est un heptadécagone,
- Un polygone à 18 côtés est un octadécagone,
- Un polygone à 19 côtés est un ennéadécagone,
- Un polygone à 20 côtés est un icosagone,
- Un polygone à 21 côtés est un henicosagone,
- Un polygone à 22 côtés est un doicosagone,
- Un polygone à 23 côtés est un triaicosagone,
- Un polygone à 24 côtés est un tétraicosagone,
- Un polygone à 30 côtés est un triacontagone,
- Un polygone à 31 côtés est un hentriacontagone,
- Un polygone à 32 côtés est un dotriacontagone,
- Un polygone à 33 côtés est un tritriacontagone,
- Un polygone à 34 côtés est un tétratriacontagone,
- Un polygone à 40 côtés est un tétracontagone,
- Un polygone à 50 côtés est un pentacontagone,
- Un polygone à 100 côtés est un hectogone,
- Un polygone à 200 côtés est un dihectogone,
- Un polygone à 300 côtés est un rihectogone,
- Un polygone à 400 côtés est un tétrahectogone,
- Un polygone à 500 côtés est un pentahectogone,
- Un polygone à 1 000 côtés est un chiliogone,
- Un polygone à 10 000 côtés est un myriagone.
Construction de quelques polygones réguliers
Le triangle équilatéral
Méthode n°1 :
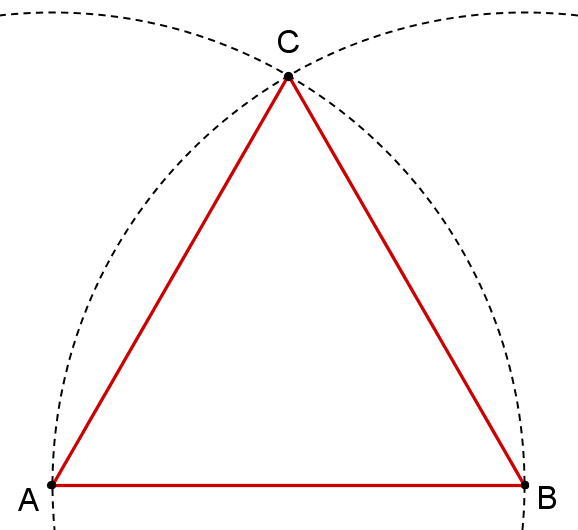
1. On place deux points distincts A et B.
2. On trace le segment [AB].
3. On trace le cercle de centre A passant par B.
4. On trace le cercle de centre B passant par A.
5. Ces deux cercles se coupent en deux points, dont l’un est noté C.
6. On trace les segments [AC] et [BC].
7. Le triangle (ABC) est équilatéral.
Méthode n°2 :
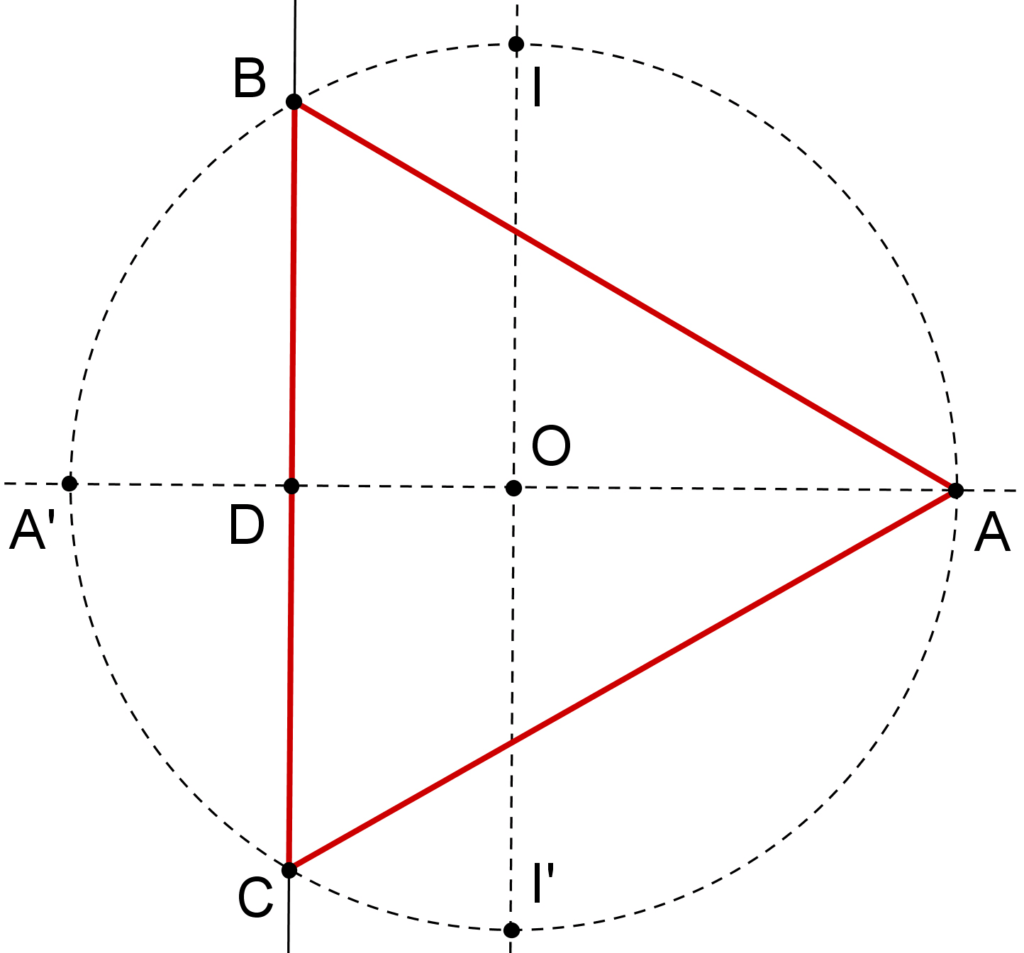
1. Dans un repère dit orthonormal (axes perpendiculaires et unités identiques sur les deux axes), on trace le cercle dit « trigonométrique », de centre O, origine du repère, et de rayon 1.
Les coordonnées (x ; y) de tout point du cercle vérifient x2 + y2 = 1, d’après le théorème de Pythagore. Ce cercle coupe les axes de coordonnées en A, A’, I et I’.
2. On trace la médiatrice de [OA’], qui coupe le cercle en B et C.
3. Le triangle (ABC) est équilatéral.
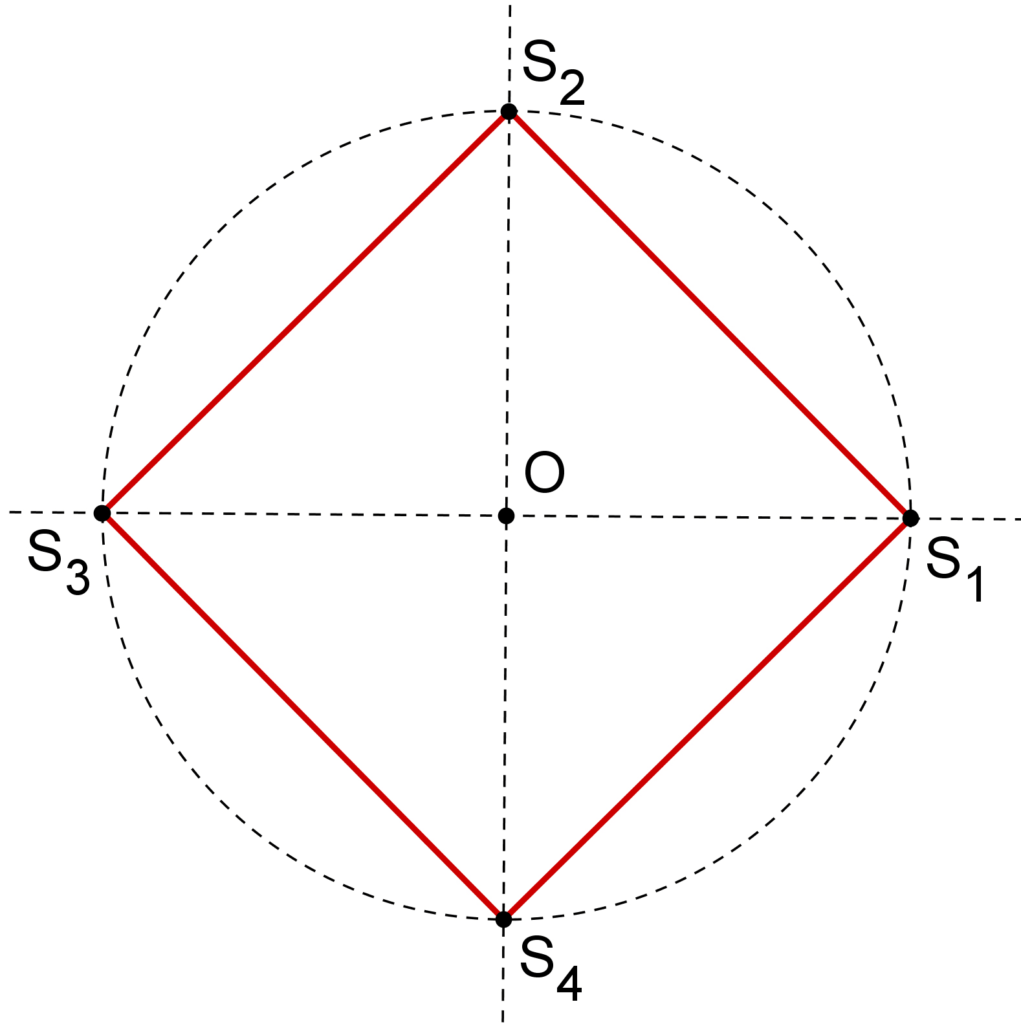
Le carré
On trace le cercle trigonométrique et on place les quatre intersections avec les axes de coordonnées. (S1S2S3S4) est un carré.
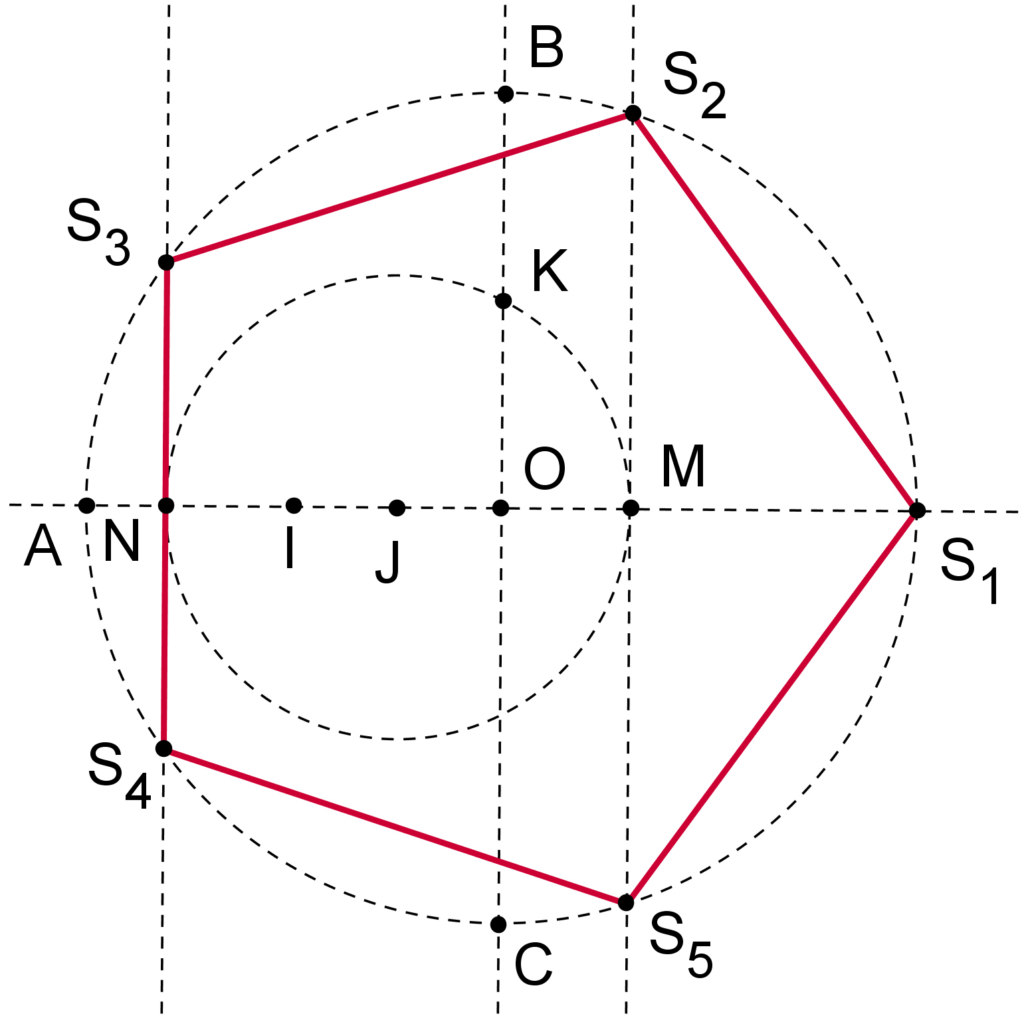
Le pentagone régulier
1. I est le milieu de [OA].
2. J est le milieu de [OI].
3. K est le milieu de [OB].
4. Le cercle de centre J passant par K coupe l’axe des abscisses en M et N.
5. Les droites parallèles à l’axe des ordonnées passant par M et N coupe le cercle trigonométrique en quatre des cinq sommets du pentagone régulier.
L’hexagone régulier
Méthode n°1 :
On peut tracer l’hexagone régulier à partir d’un triangle équilatéral.
1. On trace les trois médiatrices des trois côtés du triangle équilatéral.
2. Elles recoupent le cercle en les trois points supplémentaires servant à tracer l’hexagone régulier.
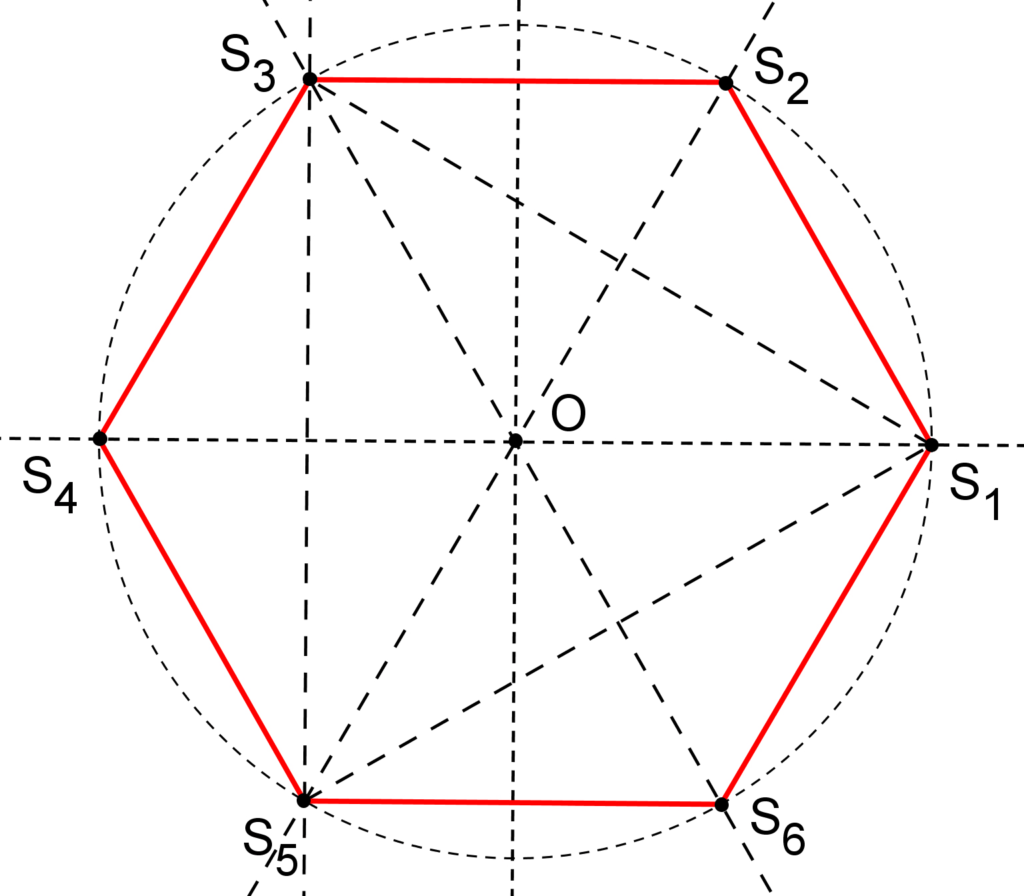
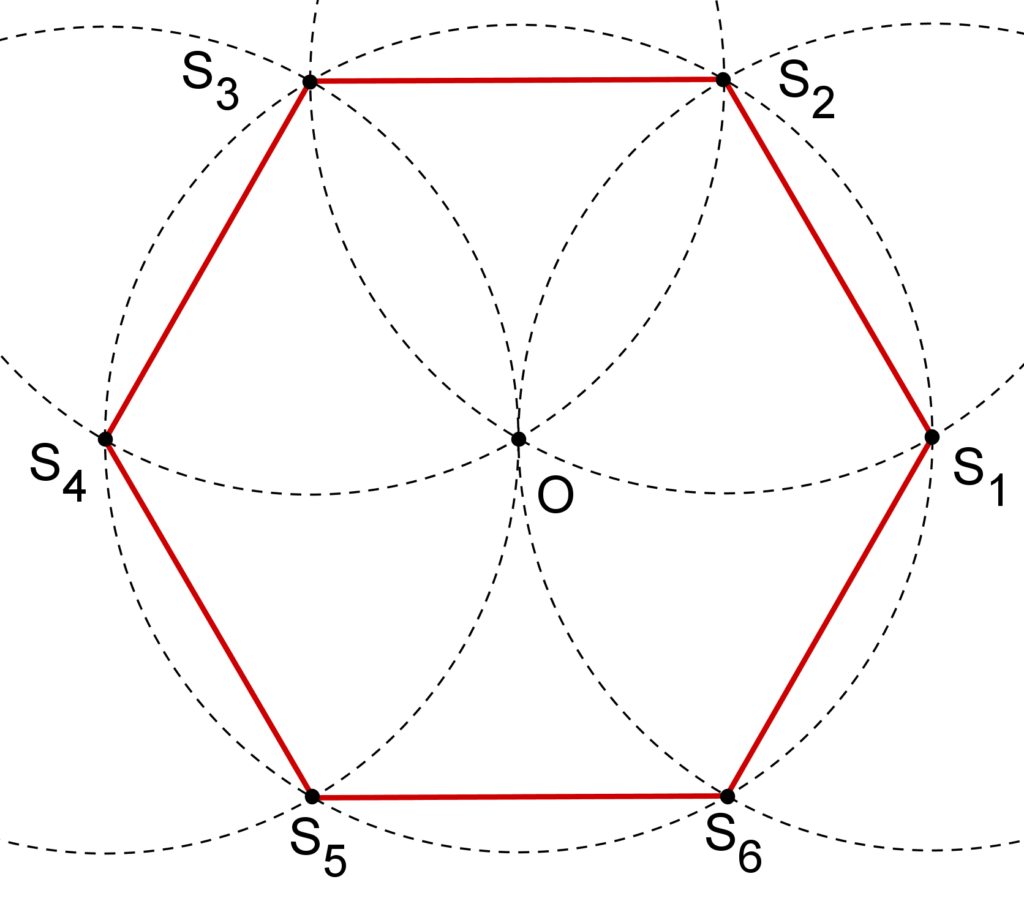
Méthode n°2 :
Une particularité (vue précédemment) de l’hexagone régulier est que la longueur du côté est égale au rayon du cercle circonscrit.
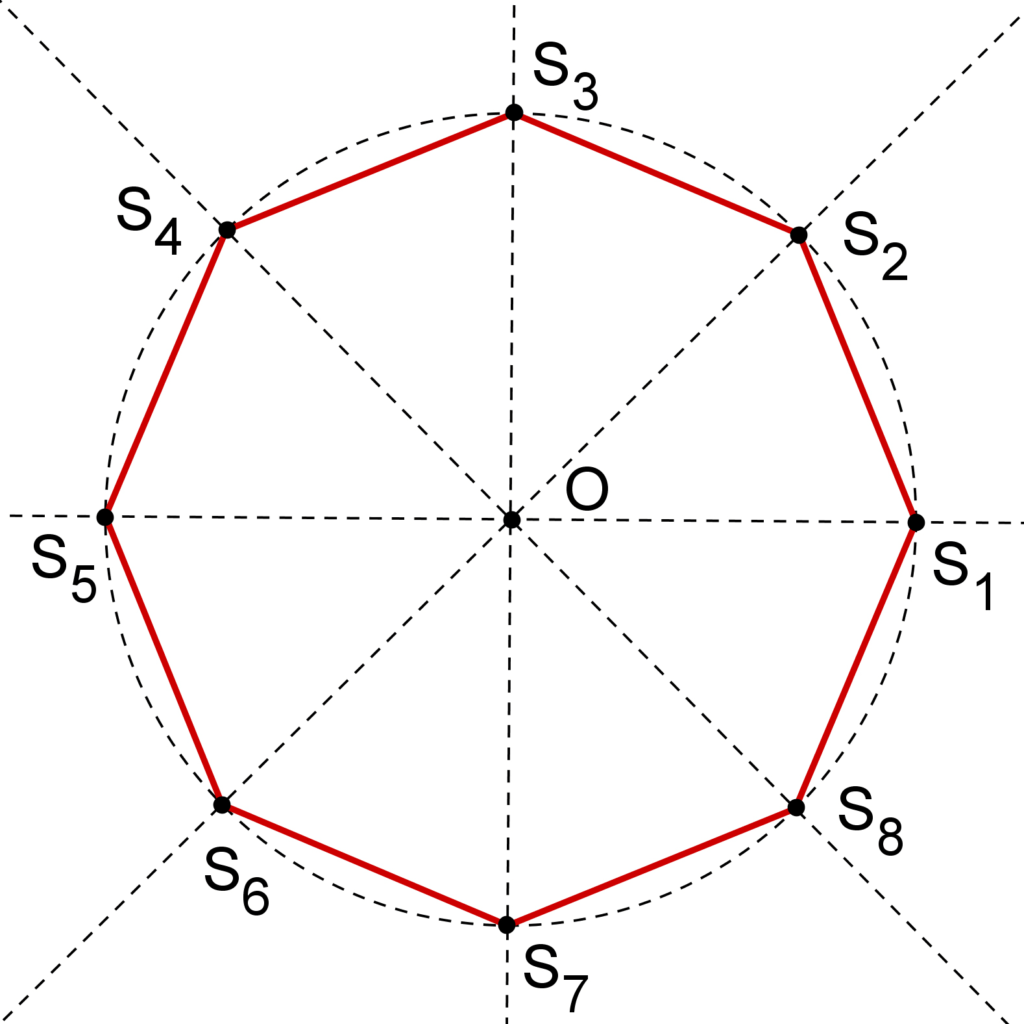
L’octogone régulier
On peut tracer l’octogone régulier à partir d’un carré.
1. On trace les quatre médiatrices des quatre côtés du carré.
2. Elles recoupent le cercle en les quatre points supplémentaires servant à tracer l’octogone régulier.
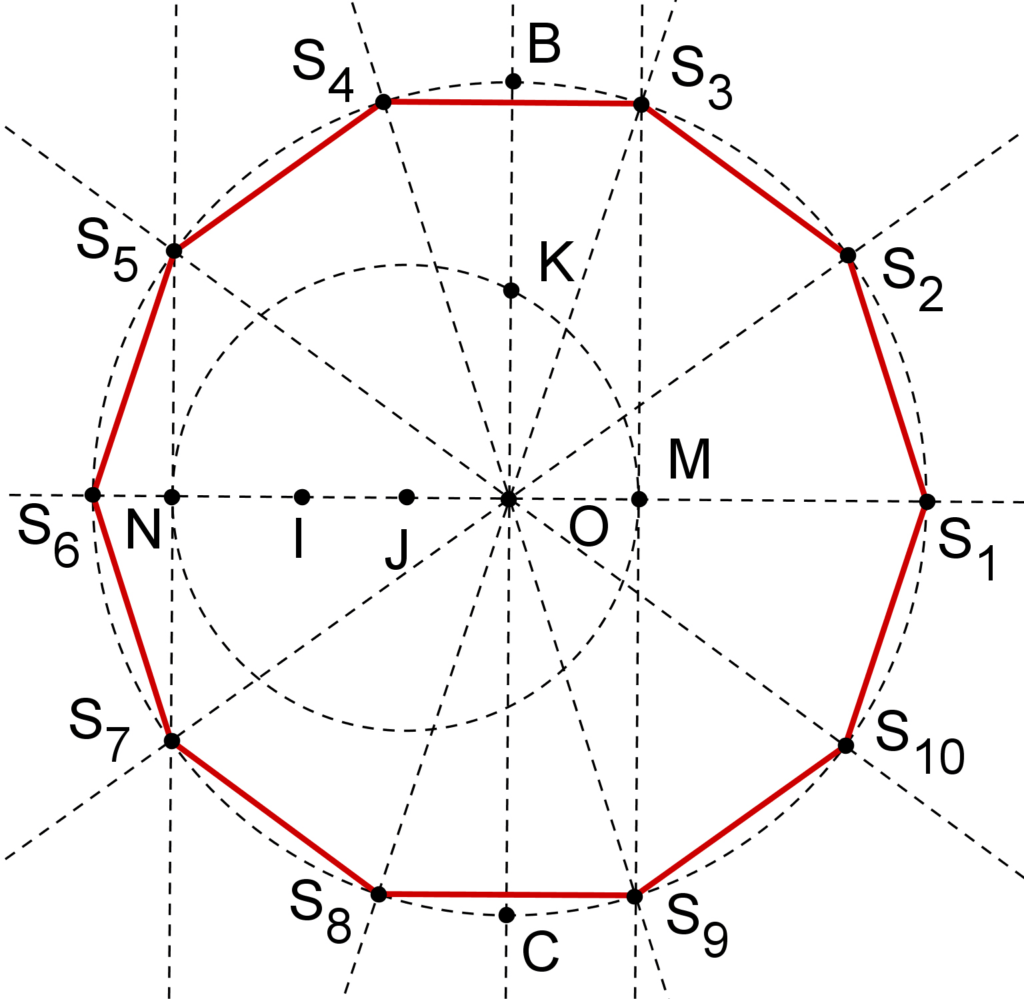
Le décagone régulier
On peut tracer le décagone régulier à partir d’un pentagone régulier.
1. On trace les cinq médiatrices des cinq côtés du pentagone.
2. Elles recoupent le cercle en les cinq points supplémentaires servant à tracer le décagone régulier.
Calcul de la somme des angles d’un polygone
La somme des mesures des angles d’un polygone à n côtés est : 180o × (n – 2)
Ainsi, par exemple :
- la somme des angles d’un triangle (3 côtés) est : 180 × (3 – 2) = 180o
- la somme des angles d’un quadrilatère (4 côtés) est : 180 × (4 – 2) = 360o
- la somme des angles d’un hexagone (6 côtés) est : 180 × (6 – 2) = 720o
- la somme des angles d’un décagone (10 côtés) est : 180 × (10 – 2) = 1440o
Calcul du nombre de diagonales d’un polygone
Le nombre de diagonales d’un polygone à n côtés est :
Nombre de diagonales = n.( n-3)/2
Comment calculer l’aire d’un polygone régulier ?
Pour calculer l’aire d’un polygone régulier on utilise la formule suivante :
A_{pr}= \frac{n\times c^{2}}{4\times tan(\frac{180^{o}}{n})}Avec
- Apr : Aire du polygone régulier
- n : Nombre de côtés ;
- c : Longueur d’un côté.
Remarque : Cette formule se base sur la découpe du polygone en triangles isocèles, elle est valable pour tous les polygones réguliers.
Voir aussi :
Autres sujets peuvent vous intéresser
Polygone régulier : Calcul en ligne, définition, construction de quelques polygones réguliers et formules
Polygone régulier : Calcul en ligne, définition, construction de quelques polygones réguliers et formules
Polygone régulier : Calcul en ligne, définition, construction de quelques polygones réguliers et formules
Polygone régulier : Calcul en ligne, définition, construction de quelques polygones réguliers et formules
Polygone régulier : Calcul en ligne, définition, construction de quelques polygones réguliers et formules
Polygone régulier : Calcul en ligne, définition, construction de quelques polygones réguliers et formules
Polygone régulier : Calcul en ligne, définition, construction de quelques polygones réguliers et formules











