
Surface d’une sphère : Calculateur, définition, propriétés et exemple de calcul
Calculateur de surface d’une sphère
Définition de la sphère
Une sphère est une figure géométrique caractérisée par deux éléments essentiels :
Son Centre et son Rayon.
Une sphère de centre le point O et de rayon R est formée de l’ensemble de tous les points M de l’espace tels que la distance OM égale le rayon de la sphère.
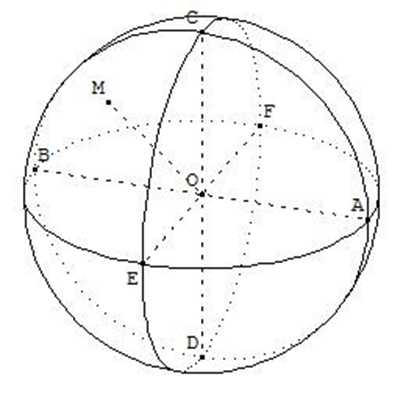
La figure ci-dessous est une représentation en perspective cavalière d’une sphère de centre O et de rayon R = OM = OA = OB = OC etc ….
Nous utiliserons la notation : S(O ; R) pour parler d’une sphère de centre O et de rayon R.
Propriétés de la sphère
La sphère elle-même est un élément géométrique avec ses propres caractéristiques. Avant d’essayer de calculer l’aire d’une sphère, résumez-les en quelques points :
- Les points à la surface de la sphère sont équidistants du centre. Le centre s’appelle “O” et le rayon s’appelle “R”.
- Le rayon est le segment de ligne entre le centre “O” et un point sur la surface.
- Le diamètre est la longueur entre deux points sur la surface d’une sphère et doit passer par le centre de la sphère. Le diamètre est le double de la longueur du rayon “R”
- Si nous traçons une ligne passant par le centre, elle divisera la sphère en deux, formant deux points diamétralement opposés.
- Si OM = R, alors le point M appartient à la sphère de centre O et de rayon R
- Si un point M appartient à une sphère de centre O et de rayon R, alors OM = R.
- Deux points A et B tels que [AB] est un diamètre de la sphère sont dits « diamétralement opposés ». En conséquence, le centre de la sphère est le milieu du segment [AB]
Comment calculer la surface d’une sphère ?
Pour calculer l’aire d’une sphère c’est simple, il suffit de prendre une mesure pour calculer l’aire ou la surface de la sphère. C’est le rayon “r”.
L’aire ou la surface d’une sphère de rayon R est donnée par la formule :
A = 4 × π × R2.
Comme le rayon vaut la moitié du diamètre, si on note par d le diamètre la formule devient :
A = π × d2.
Exemple de calcul de la surface d’une sphère
Exemple 1 :
Calculer l’aire d’une sphère de rayon 10 cm?
Réponse :
l’aire d’une sphère de rayon 10 cm est égale à :
4 × π × 102, soit 1256 cm2, avec π = 3,14.
Exemple 2 :
Calculer l’aire de la Terre au kilomètre carré près en prenant comme valeur pour le rayon de la Terre 6 370 km.
Réponse :
On a A = 4 × π × R2. Avec R = 6370 km
Application numérique : A = 4×π×63702 ≈ 509.904.363 km2
A ≈ 509.904.363 km2









