La force centripète : Calcul en ligne, définition, formule, applications et exercices corrigés
Calculateur de la force centripète
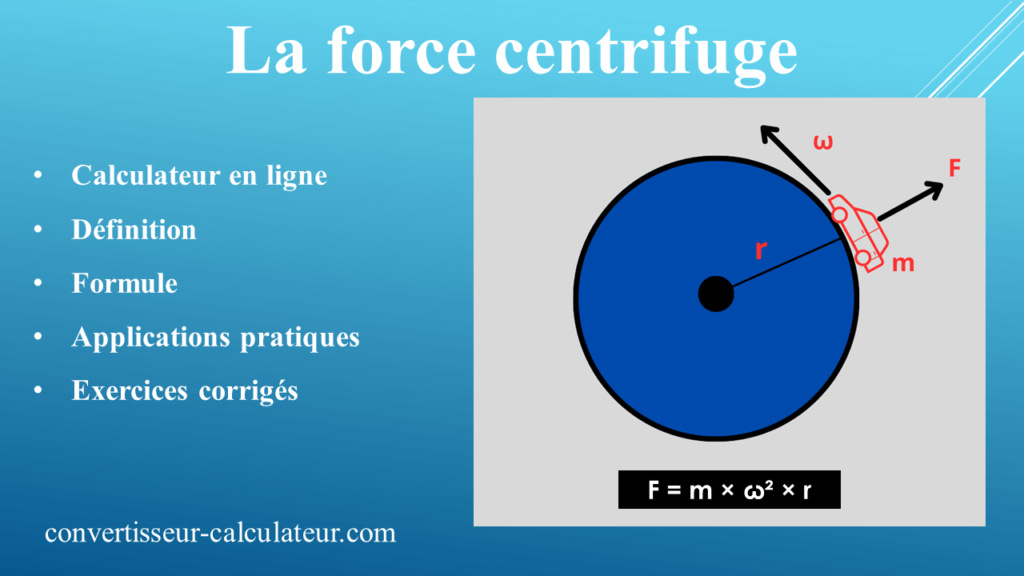
Lorsque vous faites tourner un objet au bout d’une corde, ou lorsque vous prenez un virage serré en voiture, vous pouvez ressentir une sensation de poussée ou de traction vers le centre de la trajectoire. Cette force qui maintient les objets en mouvement circulaire est connue sous le nom de force centripète. Dans cet article, nous allons explorer en détail la force centripète, son rôle, ses applications et sa relation avec d’autres concepts fondamentaux de la physique.
Qu’est-ce que la force centripète ?
La force centripète est une force dirigée vers le centre d’une trajectoire circulaire ou courbe, qui maintient un objet en mouvement sur cette trajectoire. Il est important de comprendre que la force centripète n’est pas une force physique distincte, mais plutôt le résultat d’autres forces agissant sur un objet en mouvement circulaire. La force centripète n’existe pas en soi, mais est le nom donné à la force nette qui agit vers le centre de la trajectoire circulaire.
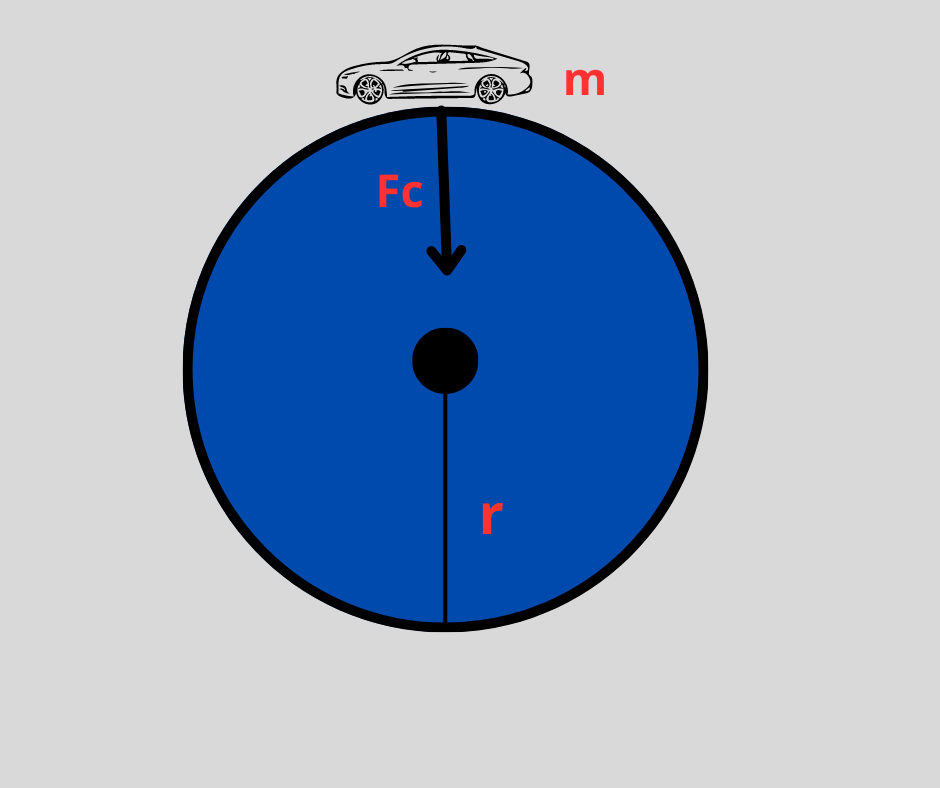
Principe de la force centripète
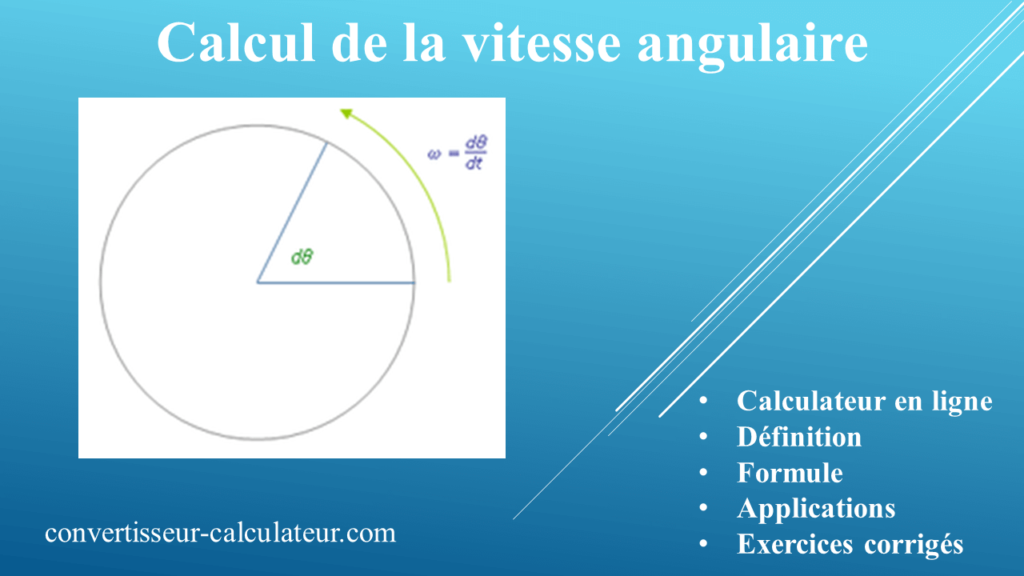
Selon la deuxième loi de Newton, la force nette (F) agissant sur un objet est directement proportionnelle à son accélération (a) et à sa masse (m), c’est-à-dire F = ma. Dans le cas d’un mouvement circulaire, un objet subit une accélération en raison du changement constant de direction. Cette accélération est appelée accélération centripète et est dirigée vers le centre de la trajectoire circulaire.
La force centripète est la force nette responsable de cette accélération centripète. Elle peut être fournie par différentes sources selon la situation, telles que la tension dans une corde, la gravité, la force électromagnétique ou toute autre force qui tire l’objet vers le centre du cercle. Quelle que soit la source de la force centripète, elle est toujours dirigée vers le centre de la trajectoire circulaire et est perpendiculaire à la vitesse de l’objet à un instant donné.
Relation avec la vitesse et le rayon
La force centripète est également liée à la vitesse et au rayon de la trajectoire circulaire. Plus précisément, la force centripète est proportionnelle à la masse de l’objet (m), au carré de sa vitesse (v) et inversement proportionnelle au rayon de la trajectoire (r). Mathématiquement, cela peut être exprimé par la formule :
Fc = (m × v²) / r
Où :
- Fc : La force centripète en newtons (N).
- m : La masse de l’objet en kilogrammes (kg).
- v : La vitesse de l’objet en mètres par seconde (m/s).
- r : Le rayon de la trajectoire circulaire en mètres (m).
Cette formule montre que la force_centripète augmente avec la vitesse au carré, ce qui signifie que des vitesses plus élevées nécessitent une force centripète plus importante pour maintenir l’objet en mouvement circulaire. De plus, la force_centripète diminue à mesure que le rayon de la trajectoire circulaire augmente.
Applications de la force centripète
La force centripète joue un rôle crucial dans de nombreux phénomènes et applications de la vie quotidienne ainsi que dans des domaines tels que la physique et l’ingénierie. Voici quelques exemples d’applications de la force centripète :
- Les manèges de fête foraine : Les manèges qui tournent en cercle, tels que les carrousels, les montagnes russes et les manèges à grande vitesse, utilisent la force_centripète pour maintenir les passagers en place et les empêcher de tomber.
- La gravité et les orbites planétaires : La force de gravité exercée par une planète sur un objet en orbite est une force centripète qui maintient l’objet en mouvement circulaire autour de la planète.
- Les courses automobiles : Les voitures qui prennent des virages serrés à grande vitesse doivent exercer une force centripète suffisante pour éviter de glisser hors de la trajectoire.
- La rotation de la Terre : La force_centripète résultant de la rotation de la Terre permet de maintenir les objets sur sa surface et de créer les effets de la gravité.
Exercices corrigés
Exercice 1 :
Un objet de masse 2 kg effectue un mouvement circulaire avec une vitesse de 4 m/s sur un rayon de 3 m. Calculez la force_centripète agissant sur l’objet.
Solution :
Données :
- m = 2 kg
- v = 4 m/s
- r = 3 m
La formule de la force centripète est : Fc = (m × v²) / r
Substituons les valeurs dans la formule :
Fc = (2 kg × (4 m/s)²) / 3 m
Fc = (2 kg × 16 m²/s²) / 3 m
Fc = 32 kg.m/s² / 3 m
Fc ≈ 10.67 N
Donc, la force_centripète agissant sur l’objet est d’environ 10.67 N.
Exercice 2 :
Un satellite artificiel de masse 500 kg est en orbite autour de la Terre. Le rayon de l’orbite est de 7000 km. Calculez la force centripète exercée sur le satellite.
Solution :
Données:
- m = 500 kg
- r = 7000000 m (7000 km)
La formule de la force_centripète est : Fc = (m × v²) / r
Dans le cas des satellites en orbite, la force centripète est fournie par la force de gravité de la Terre. Donc, nous devons utiliser la formule de la force gravitationnelle pour trouver la vitesse du satellite.
La formule de la force gravitationnelle est : Fg = G × (m1 × m2) / r²
La force gravitationnelle est équilibrée par la force centripète, donc Fc = Fg.
Donc, (m × v²) / r = G × (m1 × m2) / r²
Nous savons que m1 est la masse du satellite (500 kg) et m2 est la masse de la Terre (5.97 x 1024 kg).
v² = (G × m2) / r
v² = (6.67 x 10-11 N.m²/kg² × 5.97 x 1024 kg) / 7000000 m
v ≈ 7542.25 m/s
Maintenant, substituons les valeurs dans la formule de la force_centripète :
Fc = (m × v²) / r
Fc = (500 kg × (7542.25 m/s)²) / 7000000 m
Fc ≈ 4063.26 N
Donc, la force centripète exercée sur le satellite est d’environ 4063.26 N.
Exercice 3 :
Un pilote effectue un virage à une vitesse de 20 m/s sur une route circulaire de rayon 50 m. Calculez la force_centripète nécessaire pour maintenir la voiture sur la trajectoire.
Solution :
Données :
- v = 20 m/s
- r = 50 m
La formule de la force centripète est : Fc = (m × v²) / r
Puisque la masse de la voiture n’est pas donnée, nous pouvons la supposer comme étant égale à 1 kg (pour faciliter les calculs).
Substituons les valeurs dans la formule :
Fc = (1 kg × (20 m/s)²) / 50 m
Fc = (1 kg × 400 m²/s²) / 50 m
Fc = 8 kg.m/s²
Donc, la force centripète nécessaire pour maintenir la voiture sur la trajectoire est de 8 N.
Exercice 4 :
Un astronaute de masse 80 kg est en train de s’entraîner dans un simulateur de gravité artificielle. Le simulateur tourne à une vitesse de 10 m/s sur un rayon de 5 m. Calculez la force_centripète ressentie par l’astronaute.
Solution :
Données :
- m = 80 kg
- v = 10 m/s
- r = 5 m
La formule de la force centripète est : Fc = (m × v²) / r
Substituons les valeurs dans la formule :
Fc = (80 kg × (10 m/s)²) / 5 m
Fc = (80 kg × 100 m²/s²) / 5 m
Fc = 1600 N
Donc, la force centripète ressentie par l’astronaute dans le simulateur est de 1600 N.
Exercice 5 :
Une voiture tourne à une vitesse de 15 m/s sur un virage de rayon 30 m. Si la force centripète nécessaire pour maintenir la voiture sur la trajectoire est de 1200 N, calculez la masse de la voiture.
Solution :
Données :
- v = 15 m/s
- r = 30 m
- Fc = 1200 N
La formule de la force centripète est : Fc = (m × v²) / r
Réorganisons la formule pour résoudre la masse (m) :
m = (Fc × r) / v²
Substituons les valeurs dans la formule :
m = (1200 N × 30 m) / (15 m/s)²
m = (36000 kg.m/s²) / 225 m²/s²
m ≈ 160 kg
Donc, la masse de la voiture est d’environ 160 kg.
Conclusion
La force centripète est une force essentielle pour maintenir les objets en mouvement circulaire. Elle résulte de la combinaison d’autres forces et est dirigée vers le centre de la trajectoire circulaire. La force centripète dépend de la masse de l’objet, de sa vitesse et du rayon de la trajectoire. Comprendre la force centripète est crucial pour expliquer de nombreux phénomènes naturels et pour concevoir des systèmes impliquant un mouvement circulaire.