
Fonction trigonométrique cosinus, sinus et tangente : Calcul en ligne, définitions et propriétés
Calcul des fonctions trigonométriques
Les fonctions trigonométriques sont définies à l’aide du cercle trigonométrique :
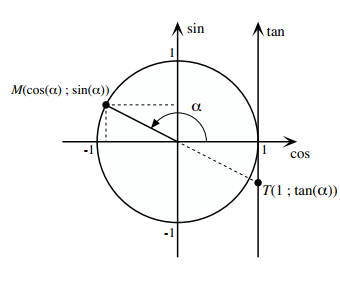
Considérons le point M du cercle trigonométrique correspondant à l’angle α.
Le cosinus de α, noté cos(α), est la 1ère coordonnée (ou abscisse) de M.
Le sinus de α, noté sin(α), est la 2ème coordonnée (ou ordonnée) de M.
La tangente de α, notée tan(α), est l’ordonnée de T.
La fonction cosinus
Définitions
La fonction qui à tout réel x, associe le réel cos(x) est appelée fonction cosinus : cos : x →cos ( x ).
Propriétés de la fonction cosinus
- Pour tout réel x, cos(-x) = cos(x). On dit que la fonction cosinus est une fonction paire. Sa courbe représentative est donc symétrique par rapport à l’axe des ordonnées.
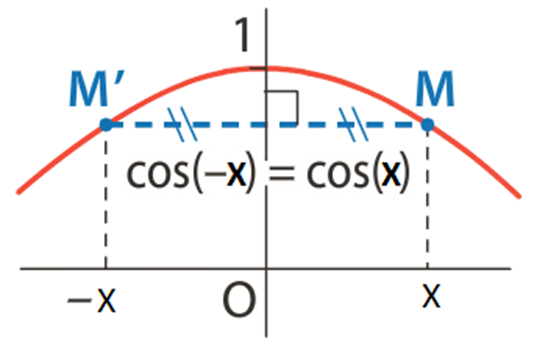
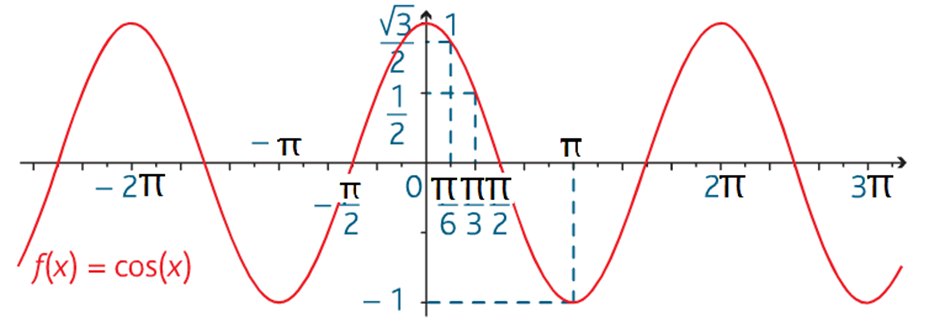
- Pour tout réel x, cos(x) = cos(x + 2π). On dit que la fonction cosinus est 2π-périodique ou périodique de période 2π. Sa courbe représentative est donc invariante par translation de vecteur 2π ou −2 π.
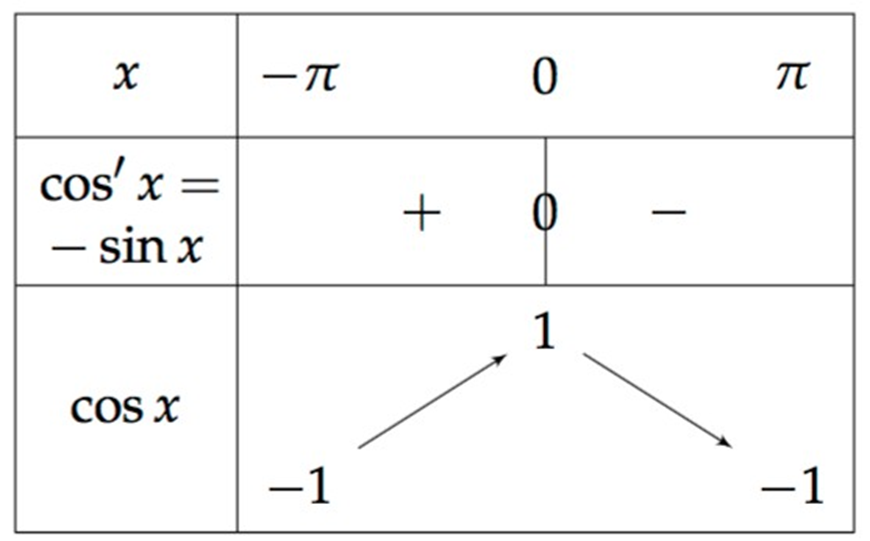
- La fonction cosinus est dérivable sur ℝ et ∀ x∈ℝ , cos ‘ ( x)=−sin ( x )
- La fonction étant 2π-périodique, on l’étudie sur un intervalle de longueur 2π , [- π ; π] par exemple
La fonction sinus
La fonction qui à tout réel x, associe le réel sin(x) est appelée fonction sinus : sin : x →sin ( x ).
Propriétés de la fonction sinus
- Pour tout réel x, sin (− x)=−sin ( x ) . On dit que la fonction sinus est une fonction impaire. Sa courbe représentative est donc symétrique par rapport à l’origine du repère.
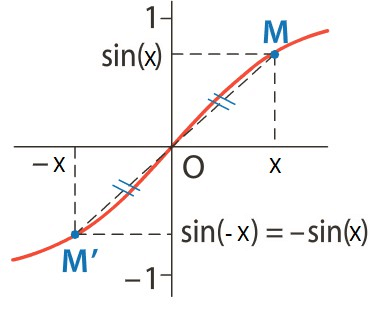
- Pour tout réel x, sin(x) = sin(x + 2π). On dit que la fonction sinus est 2π-périodique ou périodique de période 2π. Sa courbe représentative est donc invariante par translation de vecteur 2π ou −2 π.
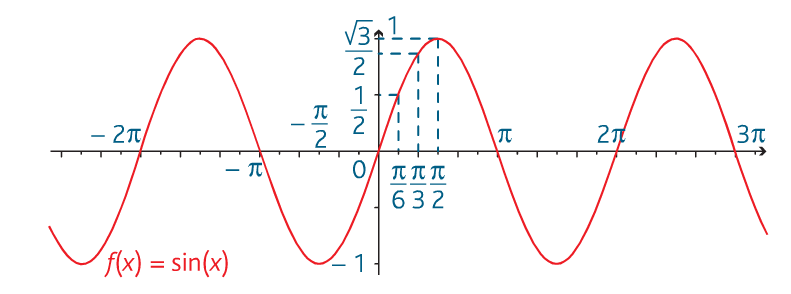
- La fonction sinus est dérivable sur ℝ et ∀ x∈ℝ , sin ‘ ( x )=cos ( x)
- Son tableau de variations : la fonction étant 2π-périodique, on l’étudie sur un intervalle de longueur 2π , [- π ; π] par exemple:
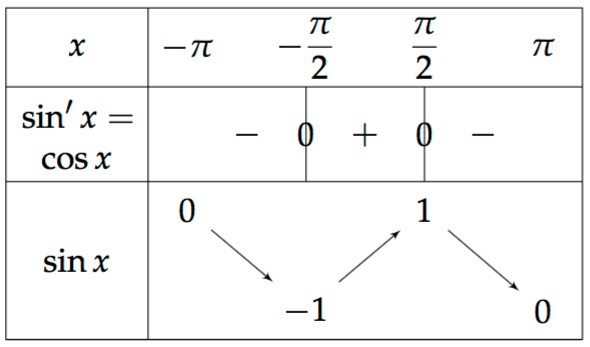
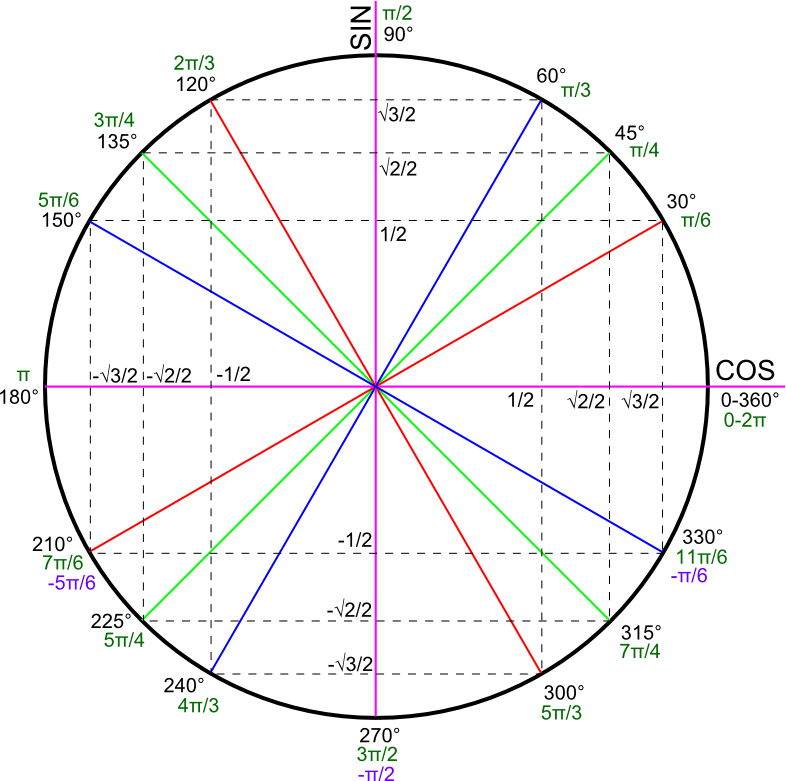
Valeurs remarquables
| Degrés | 0 | 30 | 45 | 60 | 90 | 120 | 135 | 150 | 180 |
| Radians | 0 | π/6 | π/4 | π/3 | π/2 | 2π/3 | 3π/4 | 5π/6 | π |
| Sinus | 0 | 1/2 | 1/√2 | √3/2 | 1 | √3/2 | 1/√2 | 1/2 | 0 |
| Cosinus | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1/2 | -1/√2 | -√3/2 | -1 |
Formules trigonométriques
Pour tout réel x,
- cos(−x) = cos(x)
- sin(−x) = − sin(x)
- cos(π − x) = − cos(x)
- sin(π − x) = sin(x)
- cos(π + x) = − cos(x)
- sin(π + x) = − sin(x)
- cos(π/2− x) = sin(x)
- sin(π/2− x) = cos(x)
- cos(π/2+ x) = − sin(x)
- sin(π/2+ x) = cos(x)
Formules d’addition
Pour tout réels a et b,
- cos(a + b) = cos a cos b − sin a sin b
- sin(a + b) = sin a cos b + sin b cos a
- cos(a − b) = cos a cos b + sin a sin b
- sin(a − b) = sin a cos b − sin b cos a
Formules de duplication
Pour tout réel a,
- cos 2a = cos2a − sin2a
- cos 2a = 2 cos2a − 1
- cos 2a = 1 − 2 sin2a
- sin 2a = 2 sin a cos a
- cos2 a = (1 + cos 2a)/2
- sin2 a = (1 − cos 2a)/2
Voir aussi :
Autres sujets peuvent vous intéresser
Fonction trigonométrique cosinus, sinus et tangente : Calcul en ligne, définitions et propriétés
Fonction trigonométrique cosinus, sinus et tangente : Calcul en ligne, définitions et propriétés
Fonction trigonométrique cosinus, sinus et tangente : Calcul en ligne, définitions et propriétés
Fonction trigonométrique cosinus, sinus et tangente : Calcul en ligne, définitions et propriétés
Fonction trigonométrique cosinus, sinus et tangente : Calcul en ligne, définitions et propriétés









