
Comparaison des fractions: calcul en ligne, définition, propriétés, règles et exercices corrigés
Comparaison des fractions en ligne
Définition de fraction
Une fraction est notée sous la forme d’un quotient de 2 nombres entiers. Ces deux nombres sont séparés par un trait appelé barre de fraction.
Le nombre de la partie supérieure de la fraction est le numérateur. Le nombre de la partie inférieure de la fraction est le dénominateur ( le dominateur est toujours différent de 0) .
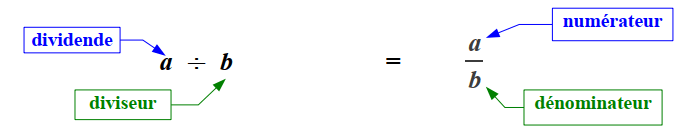
Pour lire une fraction, on lit d’abord le nombre du numérateur puis le nombre du dénominateur auquel on ajoute le suffixe « ièmes ».
Exemples :
- 4/7 : se lit quatre septièmes.
- 3/10 : se lit trois dixièmes.
Exceptions :
- ½ : se lit un demi.
- 1/3 se lit un tiers.
- 1/4 se lit un quart.
Propriétés des fractions
- Si le numérateur est inférieur au dénominateur, alors la fraction est inférieure à 1.
- Si le numérateur est supérieur au dénominateur, alors la fraction est supérieure à 1.
- Si le numérateur et le dénominateur sont égaux, alors la fraction est égale à 1.
- Le dénominateur doit toujours être différent de 0, car la division par 0 est indéfinie en mathématique.
Comment comparer les fractions ?
Définition
Comparer deux nombres signifie dire lequel est le plus grand, lequel est le plus petit, ou s’ils sont égaux.
On utilise les symboles < (“est inférieur à”, “est plus petit que”), > (“est supérieur à”, “est plus grand que”) et = (“est égal à”)
Comparer deux fractions ayant le même dénominateur
Si deux nombres en écriture fractionnaire ont le même dénominateur, alors ils sont rangés dans le même ordre que leurs numérateurs.
Exemples :
- 5/7 < 8/ 7car 5 < 8.
- 13 /11 > 8 /11 car 13 > 8.
Comparer deux fractions ayant le même numérateur
Si deux nombres en écriture fractionnaires ont le même numérateur, alors ils sont rangés dans l’ordre inverse leurs dénominateurs.
Exemples :
- 5/7 > 5/ 9 car 7 < 9.
- 13 /11 > 13 /15 car 11 < 15.
Comparer deux fractions, le dénominateur de l’une étant un multiple du dénominateur de l’autre
On commence par réduire les deux fractions au même dénominateur, avant d’appliquer la règle 1.
Exemple :
Comparons 5/7 et 9/14 :
on\quad a\quad\frac{5}{7}= \frac{5\times 2}{7\times 2}= \frac{10}{14};\quad or \quad \frac{10}{14}> \frac{9}{14} \quad donc \quad \frac{5}{7}> \frac{9}{14}Comparer deux fractions en les comparants à un même nombre entier
- Si le numérateur d’un nombre en écriture fractionnaire est inférieur à son dénominateur, alors ce nombre est inférieur à 1.
- Si le numérateur d’un nombre en écriture fractionnaire est supérieur à son dénominateur, alors ce nombre est supérieur à 1.
Exemple
Comparons 5/7 et 9/8 :
On a 5/7 < 1 car 5 < 7 ; de plus 9 /8 > 1 car 9 > 8 donc 5/7 < 9/8.
Exercice corrigé sur la comparaison des fractions
Dans chaque cas, comparer les deux nombres en détaillant la technique utilisée :
a. 4/3 et 11/9.
b. 2/5 et 9/20.
c. 4/7 et 23/28.
d. 17/4 et 16/3.
e. 7/4 et 4/7.
f. 26/18 et 62/45.
Réponse
a. 4/3 et 11/9 :
on\quad a\quad\frac{4}{3}= \frac{4\times 3}{3\times 3}= \frac{12}{9};\quad or \quad \frac{12}{9}> \frac{11}{9} \quad donc \quad \frac{4}{3}> \frac{11}{9}b. 2/5 et 9/20 :
on\quad a\quad\frac{2}{5}= \frac{2\times 4}{5\times 4}= \frac{8}{20};\quad or \quad \frac{8}{20}< \frac{9}{20} \quad donc \quad \frac{2}{5}< \frac{9}{20}c. 4/7 et 23/28 :
on\quad a\quad\frac{4}{7}= \frac{4\times 4}{7\times 4}= \frac{16}{28};\quad or \quad \frac{16}{28}< \frac{23}{28} \quad donc \quad \frac{4}{7}< \frac{23}{28}d. 17/4 et 16/3 :
\frac{17}{4}\approx 4 \quad et \quad \frac{16}{3}\approx 5 \quad donc \quad \frac{17}{4}< \frac{16}{3}e. 7/4 et 4/7 :
7> 4 \quad donc \quad \frac{7}{4}> 1 \quad ; \quad 4 < 7 \quad donc \quad \frac{4}{7}< 1 \quad d'ou \quad \frac{7}{4}> \frac{4}{7}f. 26/18 et 62/45 :
\frac{26}{18}\approx 1.4 \quad et \quad \frac{62}{45}\approx 1.3 \quad donc \quad \frac{26}{18}> \frac{62}{45}Voir aussi :
Autres sujets peuvent vous intéresser
Comparaison des fractions: calcul en ligne, définition, propriétés, règles et exercices corrigés
Comparaison des fractions: calcul en ligne, définition, propriétés, règles et exercices corrigés
Comparaison des fractions: calcul en ligne, définition, propriétés, règles et exercices corrigés
Comparaison des fractions: calcul en ligne, définition, propriétés, règles et exercices corrigés
Comparaison des fractions: calcul en ligne, définition, propriétés, règles et exercices corrigés









