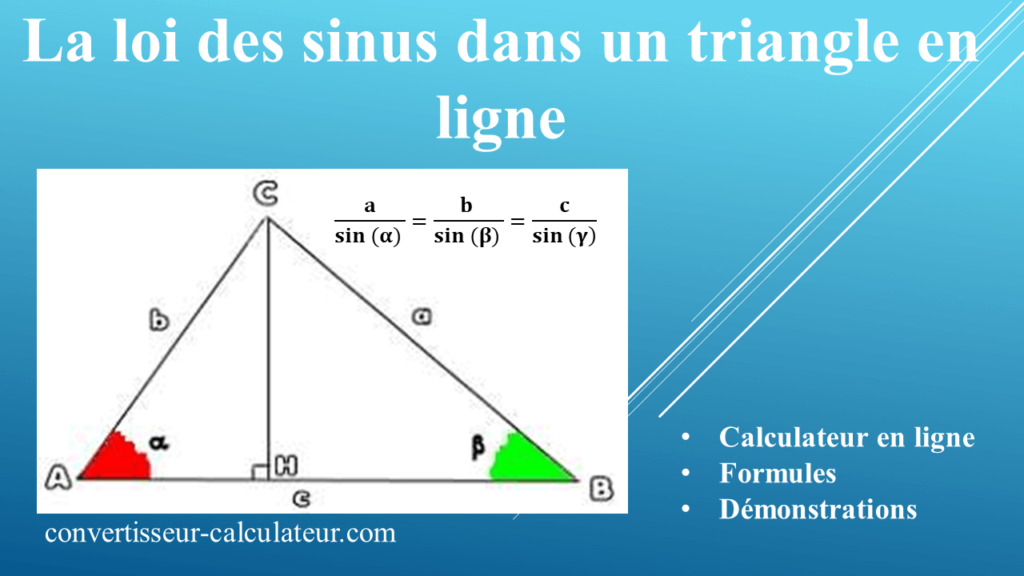
Loi des sinus dans un triangle : Calculateur en ligne, Formules et démonstration
Calculateur de la loi des sinus
La loi des sinus
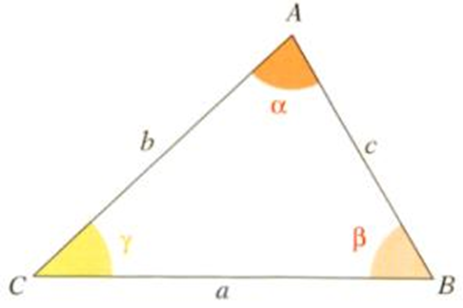
Dans un triangle quelconque ABC, les rapports entre la mesure du côté et le sinus de l’angle opposé sont égaux.
𝑎 /sin (𝛼) = 𝑏 /sin (𝛽) = 𝑐/sin (𝛾) ou sin(𝛼) / 𝑎 = sin(𝛽) / 𝑏 = sin(𝛾) / 𝑐
Avec :
- 𝑎, la mesure du côté [CB]
- 𝑏, la mesure du côté [AC]
- 𝑐, la mesure du côté [AB]
Démonstration
Considérons un triangle ABC dont les côtés [AB], [BC] et [CA] mesurent respectivement c, a et b. Soit H le pied de la hauteur issue de C.
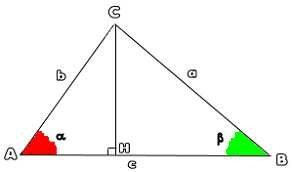
1. En utilisant le triangle AHC rectangle en H, montrer que : CH = b sin α
2. En utilisant le triangle BHC rectangle en H, montrer que : CH = a sin β
3. Montrer alors que : 𝑎 /sin (𝛼) = 𝑏 /sin (𝛽)
4. Soit K le pied de la hauteur issue de A. En reprenant la méthode précédente, montrer que : 𝑏 /sin (𝛽) = 𝑐/sin (𝛾)
5. Conclure que : 𝑎 /sin (𝛼) = 𝑏 /sin (𝛽) = 𝑐/sin (𝛾)
Correction :
1 . En utilisant le triangle AHC rectangle en H, montrer que : CH = b sin α.
Dans le triangle AHC rectangle en H, nous avons :
sin (𝛼) = CH / AC
sin (𝛼) = CH / b
D’où CH = b.sin (𝛼)
2. En utilisant le triangle BHC rectangle en H, montrer que : CH = a sin β
Dans le triangle AHC rectangle en H, nous avons :
sin (𝛽) = CH / BC
sin (𝛽) = CH / a
D’où CH = a.sin (𝛽)
3. Montrer alors que : 𝑎 /sin (𝛼) = 𝑏 /sin (𝛽)
Des deux premières questions, nous avons :
CH = b.sin (𝛼) et CH = a.sin (𝛽)
Donc a.sin (𝛽) = b.sin (𝛼)
D’où :
𝑎 /sin (𝛼) = 𝑏 /sin (𝛽)
4. montrer que : 𝑏 /sin (𝛽) = 𝑐/sin (𝛾)
Soit K le pied de la hauteur issue de A. En considérant les deux triangles CAK et BAK, nous obtenons, comme précédemment :
AK = b.sin (𝛾) et AK = c.sin (𝛽)
Et par suite :
𝑏 /sin (𝛽) = 𝑐/sin (𝛾)
5. Conclusion :
On a 𝑏 /sin (𝛽) = 𝑐/sin (𝛾) et 𝑎 /sin (𝛼) = 𝑏 /sin (𝛽)
Alors :
𝑎 /sin (𝛼) = 𝑏 /sin (𝛽) = 𝑐/sin (𝛾)
Voir aussi :
Autres sujets peuvent vous intéresser
Loi des sinus dans un triangle : Calculateur en ligne, Formules et démonstration









