La Valeur absolue : Calculateur en ligne, Définition, propriétés, Variations de la valeur absolue, Distance entre deux réels et exercices corrigés
Calculateur de la valeur absolue
La valeur absolue est utilisée pour traduire des situations de la vie courante telles que les distances. Elle intervient aussi dans certains domaines tels que l’analyse (calculs de limites et intégral), l’algèbre (résolutions d’équations et d’inéquations, nombres complexes), les sciences physiques (calculs d’incertitudes sur les mesures, calculs de vitesses).
Définition de la valeur absolue
On appelle fonction valeur absolue, la fonction définie sur IR, qui a tout réel x associe le réel noté |x| tel que :
- Si x est positif ou nul |x| = x
- Si x est négatif |x| = -x (l’opposé de x)
Exemples :
- |4|= 4 ;
- |-3|= 3 ;
- |1 – √3 |= – (1 – √3) = √3 – 1 ;
- |x – 2|= x – 2 si x ≥ 2 ;
- |x – 2|= -x + 2 si x ≤ 2.
Propriétés de la valeur absolue
- La valeur absolue d’une quantité A est un nombre positif. |A| ≥ 0 pour tout A dans IR ;
- Une quantité A dont la valeur absolue est nulle est nulle. |A| = 0 entraine A = 0 ;
- Deux quantités dont les valeurs absolues sont égales sont soit égales soit opposées. |A| = |B| entraine A = B ou A = –B ;
- La valeur absolue d’un produit est égale au produit des valeurs absolues. |AB| = |A|.|B| ;
- La valeur absolue d’un quotient est égale au quotient des valeurs absolues. |A/B| = |A|/|B| lorsque B ≠ 0 ;
- La valeur absolue d’une somme est inférieure ou égale à la somme des valeurs absolues. |A + B| ≤ |A| + |B| Inégalité triangulaire.
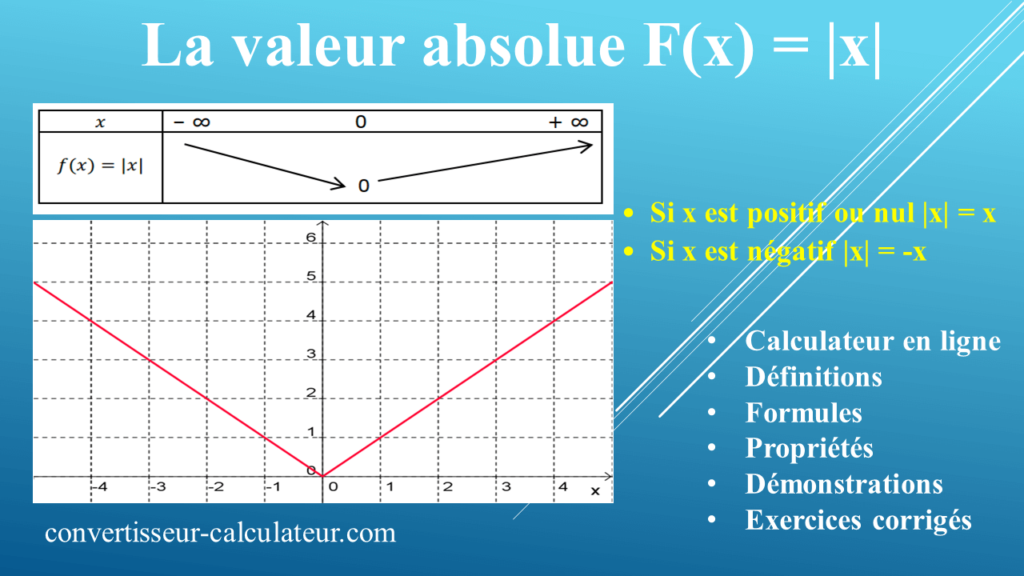
Variations de la fonction valeur absolue sur IR
D’après la définition de la fonction |x| on a sur ] –∞ ; 0] |x| = -x et sur [ 0 ; + ∞[ ݂|x| = x.
La fonction valeur absolue est donc strictement décroissante sur ]–∞ ; 0], et strictement
croissante sur [0 ; + ∞[.
Tableau de variations de la fonction |x|
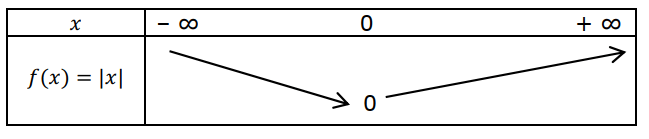
Représentation graphique de la fonction |x|.
- La courbe de la fonction |x| coïncide sur ] –∞ ; 0] avec la demi droite d’équation y = – x et sur [0 ; + ∞[ avec la demi droite d’équation y = – x.
- La courbe de la fonction |x| admet donc (en repère orthogonal) l’axe des ordonnées comme axe de symétrie. La fonction |x| est dite paire.
Distance entre deux réels
Définition
Soit x et y deux réels.
On appelle distance entre les réels x et y la distance entre les points d’abscisses x et y sur la droite graduée. On notera cette distance d (x ; y).
Propriété
La distance entre deux réels est la différence entre le plus grand et le plus petit, c’est-à-dire :
- Si x ≥ y, d (x ; y) = x − y
- Si x ≤ y, d (x ; y) = y – x
Démonstration :
Si x ≥ y : donc d (x ; y) = x − y et, comme x − y ≥ 0, |x − y| = x − y.
On a donc bien dans ce cas d (x ; y) = |x − y|.
Si x ≤ y : donc d (x ; y) = y − x et, comme x − y ≤ 0, |x − y| = − (x − y) = −x + y = y − x.
On a donc bien dans ce cas d (x ; y) = |x − y|.
Exercice corrigés
Exercice N°1 :
Effectuer les calculs suivants :
a. |2×3 − 7| ; b. |√2 − √3| ; c. 2× |3 × 1/4− 2|+ 1 ; d.|3 − π| ; e. |2×|2×5 − 12| − 7|
Correction
a. |2×3 − 7| = |−1| = 1
b. Nous savons que √2<√3. Ainsi, √2−√3 est un nombre négatif. On en déduit : |√2 − √3| = −(√2 − √3) = √3 − √2
c. 2× |3 × 1/4 − 2|+ 1 = 2× |3/4 − 2| + 1 = 2× |−5/4| + 1 = 2 × 5/4 + 1 = 10/4 + 1 = 14/4 = 7/2.
d. Sachant que π>3, le nombre 3−π est négatif. On en déduit : |3 − π| = π − 3
e. |2×|2×5 − 12| − 7| = |2×|−2| − 7| = |2×2 − 7| =|− 3|= 3.
Exercice N°2 :
Résoudre l’équation suivante : 2x − 2| = |x + 3|.
Correction
La résolution de l’équation 2x−2 = x+3 se traduit par la résolution des deux équations suivantes :
- Equation 1 :
2x − 2 = x + 3
2x − x = 3 + 2
x = 5
- Equation 2 :
2x − 2 = −(x + 3)
2x − 2 = −x − 3
2x + x = −3 + 2
3x = −1
x = −1/3
Cette équation admet pour ensemble de définition :
S = {−1/3 ; 5}









