
Force de frottement : calcul en ligne, définitions, propriétés et exercices corrigés
Calcul de la force de frottement
Frottements statiques
Le frottement statique est une force FFS qui empêche un mouvement de démarrer. C’est lui qui nous permet, en s’appuyant sur le sol, d’avancer et de tenir la route dans un virage. La bicyclette se déplace vers l’avant quand le pneu arrière pousse sur la route, vers l’arrière, grâce au frottement. Par réaction, le sol pousse le pneu vers l’avant, et par la suite le vélo et son cycliste.
Le frottement statique n’est pas consommateur d’énergie puisqu’il ne s’accompagne d’aucun déplacement sauf en cas de dérapage, mais l’on parle alors de frottement cinétique. La force maximale de frottement statique FFSmax, au-delà de laquelle il y a glissement, est proportionnelle à la force normale FN selon un coefficient de frottement statique µs dépendant des deux matériaux en contact.
FFSmax = µs × FN
Frottements cinétiques
Le frottement cinétique est la force qui tend à freiner un corps glissant sur une surface. Cette force FFC est égale et de sens opposé à la force motrice nécessaire pour maintenir le corps en mouvement uniforme. Elle est donnée par la formule FFC = µc ×FN , dans laquelle µc est le coefficient de frottement cinétique. Le frottement cinétique est habituellement inférieur au frottement statique. Cela veut dire qu’il faut une force plus grande pour vaincre l’adhérence (due au frottement statique) que pour entretenir le glissement consécutif à la perte d’adhérence. Une fois que la roue est partie…
Le frottement cinétique diminue souvent, mais pas toujours comme nous allons en voir une illustration au paragraphe suivant, lorsque la vitesse de glissement augmente. Nous avons tous constaté qu’il fallait lâcher les freins au fur et à mesure que la vitesse diminuait, pour ne pas s’arrêter brutalement ou voir une roue déraper.
Parce qu’il y a mouvement, les frottements cinétiques, contrairement aux frottements statiques, consomment de l’énergie du cycliste et la transforment en énergie thermique. Les pièces en frottement l’une contre l’autre chauffent, nous le savons d’expérience.
Le coefficient de frottement statique µs
Prenons l’exemple du frottement statique entre la route et les pneus. Le premier matériau est le goudron de la route, ou la terre et les cailloux du chemin muletier. Il y a différentes textures du bitume ou qualités du chemin. Le deuxième matériau est le pneu. Ses propriétés varient selon la gomme, la chape… Dans ce domaine, le choix est infini. De plus, l’état d’un matériau peut changer selon les circonstances. Le coefficient de frottement statique d’un pneu sur du bitume sec est plus élevé que celui d’un pneu sur du goudron mouillé. Il l’est encore moins si la route est verglacée ou peinte et humide comme sur les passages pour piétons.
FFSmax est indépendante de la valeur de la surface de contact entre deux corps solides. Donc, entre le goudron et le pneu que l’on assimile à un corps solide. À qualité de gomme égale, la tenue de route n’est pas meilleure avec des pneus de 700, de 650 ou de 26 pouces, avec des pneus de faible section ou des gros boudins.
Propriétés des coefficients de frottements
Le Coefficient de frottement dépendent de :
- Nature des corps en contact
- Etat des surfaces (rugueux ou poli, sec ou lubrifié, …)
- Température
Le Coefficient de frottement ne dépendent pas de :
- Vitesse (si v ≠ 0).
- Dimension des surfaces de contact (si surfaces planes)
En règle générale µc < µs
Quelques valeurs des coefficients de frottements µs et µc
| Corps en contact | µs | µc |
| Acier sur acier (sec) | 0.78 | 0.42 |
| Acier sur acier (gras) | 0.10 | 0.05 |
| Acier sur acier (surfaces polies) | 100 | 100 |
| Bois sur bois | 0.50 | 0.30 |
| Métal sur glace | 0.03 | 0.01 |
| Pneu sur route sèche | 0.80 | 0.60 |
| Pneu sur route mouillée | 0.15 | 0.10 |
| Téflon sur téflon | 0.04 | 0.04 |
| Cuir sur fonte | 0.28 | 0.56 |
La force normale FN
La force exercée par la route sur le cycliste et son vélo est appelée force de réaction Froute. Elle part du point de contact entre la route et les deux pneus. Dans un plan orthogonal à la trajectoire, on peut décomposer Froute en deux forces : La première force est la force normale FN qui est perpendiculaire à la route. Si la surface de la route est horizontale, la force normale est verticale. Elle est alors, répartie sur les deux roues, égale et opposée à la force du poids FP de la bicyclette et du cycliste, par définition toujours verticale.
La deuxième force est tangente à la surface. C’est une force de frottement. Elle est nulle sur une route horizontale dans une trajectoire rectiligne. Dans un virage, elle est dirigée vers l’intérieur de la courbe. C’est elle qui s’oppose au glissement du pneu. La force de réaction de la route est liée au poids du cycliste et du vélo et augmente avec lui. Donc, plus le cycliste est lourd ou chargé, plus la force maximale de frottement statique est élevée.
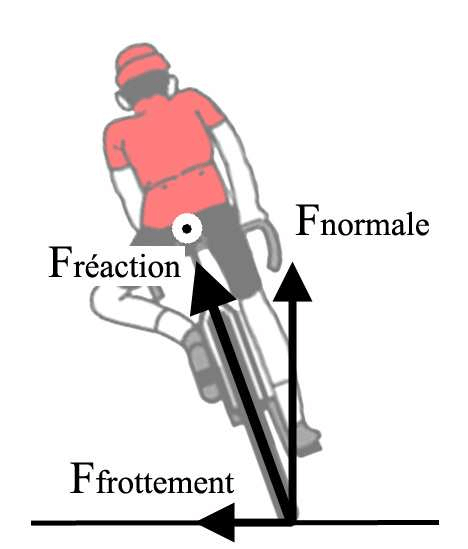
Exercices corrigés sur la force de frottement.
Exercice 1
On pousse une caisse afin de la déplacer le long du sol. Le coefficient de frottement cinétique entre une caisse de 35 kg et le sol est 0,31.
m=35 kg μc=0,31 a =0,5 m⁄s2 Fa=?
Solution
Étape 1 : Diagramme de forces :
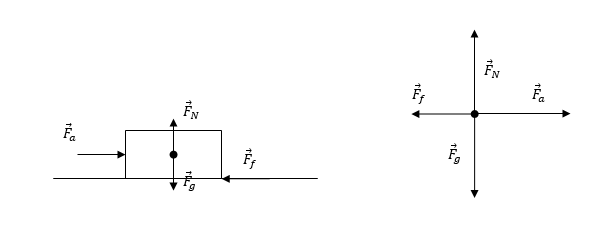
Étape 2 : Calcul de la force de frottement. Afin de calculer la force de frottement, il faut premièrement calculer la force normale, qui est égale à la force gravitationnelle mais dirigée vers le haut.
- Fg= m×g =35 kg×9,8 N⁄kg=343 N
- Ff= μc×FN = 0,31×343 N = 106,33 N
Exercice 2
Une personne en fauteuil roulant voyage vers le haut d’un trottoir incliné. La masse totale de la personne et du fauteuil roulant est 65,0 kg. Le coefficient de frottement du trottoir a une valeur de 0,11. Le degré d’inclinaison de la pente est 7,0o. Calculer la force de frottement.
m=65,0 kg μc=0,11 θ=7,0°
Solution
Étape 1 : Diagramme de forces :
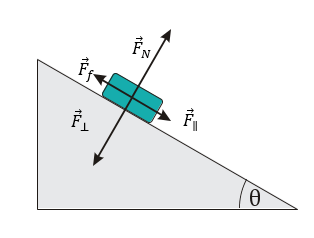
Étape 2 : Calcul des composantes de la force normale
- Force gravitationnelle : Fg=m×g =65 kg×9,8 N⁄kg=637 N=640 N
- Force normale : F⊥ = FN = Fg . cos(θ) = 640 N × cos (7,0°) = 635 N
Étape 3 : Calcul du frottement
Ff = μc×FN= 0,11×635 N=69,85 N
Voir aussi :
Autres sujets peuvent vous intéresser
Force de frottement : calcul en ligne, définitions, propriétés et exercices corrigés
Force de frottement : calcul en ligne, définitions, propriétés et exercices corrigés
Force de frottement : calcul en ligne, définitions, propriétés et exercices corrigés
Force de frottement : calcul en ligne, définitions, propriétés et exercices corrigés
Force de frottement : calcul en ligne, définitions, propriétés et exercices corrigés
Force de frottement : calcul en ligne, définitions, propriétés et exercices corrigés









