
Prisme droit : Calculateur d’aire, définition, représentation, formules et exemples de calculs
Calculateur d’aire du prisme droit
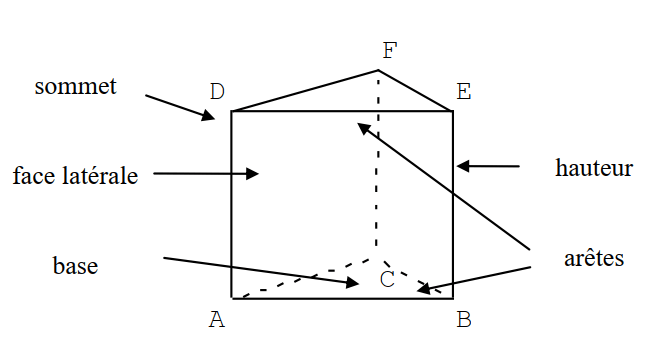
Définition du prisme droit
Un prisme droit est un solide dont :
- Les deux bases sont des polygones (triangles, quadrilatères…). Elles sont parallèles.
- Les autres faces sont des rectangles et sont appelées les faces latérales : ABED , ACFD et BCFE.
- L’arête [AD] est perpendiculaire à la face ABC
- La distance entre les deux bases, c’est à dire AD ou BF ou CF est appelée hauteur du prisme droit.
Remarque : Le pavé droit (parallélépipède rectangle) est un prisme droit particulier : ses deux bases sont aussi des rectangles.
Représentation en perspective cavalière
Représenter en perspective cavalière un prisme droit à base triangulaire
Étape 1 : On trace deux triangles superposables (les bases du prisme) en utilisant le quadrillage.
Étape 2 : On relie les sommets en dessinant les arêtes manquantes.
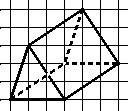
Remarques :
- Les arêtes cachées sont en pointillés.
- Deux arêtes perpendiculaires ne sont pas toujours représentées par des segments perpendiculaires !!!
- Deux droites parallèles dans la réalité sont représentées par deux droites parallèles.
Comment calculer l’aire d’un prisme droit ?
Aire latérale
Pour calculer l’aire latérale d’un prisme droit, on multiplie le périmètre d’une base par la hauteur :
Alatérale = Pbase × h.
Aire totale
L’aire totale d’un prisme est la somme d’aire Latérale et celle de bases.
Aire totale =2 x (aire de base) + (aire latérale)
Atotale = 2× Abase + Alatérale.
Exemple 1
Détermine l’aire latérale d’un prisme droit de hauteur 10 cm ayant pour base un parallélogramme ABCD tel que AB = 5 cm et BC = 3 cm.
On calcule le périmètre du parallélogramme ABCD qui est une base du prisme droit :
Pbase = 2 × (AB + BC) = 2 × (5 cm + 3 cm) = 2 × 8 cm = 16 cm.
On multiplie le périmètre d’une base par la hauteur :
Alatérale = Pbase × h = 16 cm × 10 cm = 160 cm2.
L’aire latérale de ce prisme droit vaut 160 cm²
Exemple 2
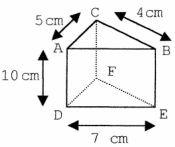
Calculer l’aire latérale de ce prisme droit à base triangulaire.
Aire latérale = Périmètre de ABC × Hauteur [AD]
= (AB + BC + CA) × AD
= (7 + 4 + 5) × 10
= 160 cm
Exemple 3
La barre de chocolat ci-dessous, a la forme d’un prisme droit qui a pour base triangulaire isocèle. Calculer la surface minimale du papier pour couvrir cette barre de chocolat.
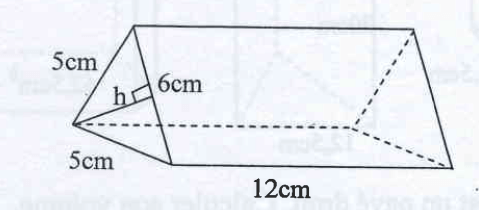
On applique la Théorème de Pythagore on a : h2 =52 -(6\2)2 =25-9=16
Donc h = 4cm
– L’aire de deux bases : Sbases = 2x (1/2 x 6×4) =24cm2
La surface latérale de cette barre :
Slaterale= (5+5+6) × 12 = 192Cm2
– La surface totale de cette barre :
Stotale= Slaterale + Sbases =24+192=2l6cm2
Donc pour couvrir cette barre de chocolat, il faut du papier d’aire 216 cm2 au minimum.









